Некоторые задачи оптимизации в экономике

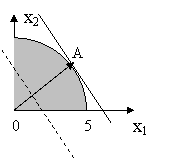
нкции L: x1+2x2=C. Выразим x2=. Линиями уровня будут параллельные прямые с угловым коэффициентом, равным -. Минимум функции достигается в точке (0;0), Lmin=0, т.к. градиент (1,2) направлен вверх вправо. Максимум достигается в точке касания кривой х2= и линии уровня. Т.к. угловой коэффициент касательной к графику функции равен -, найдём координаты точки касания, используя геометрический смысл производной.

=-; ()=-;

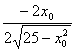=-; x0=; x2=2.

Тогда L=+2∙2=5.

Ответ: Минимум достигается в точке О(0;0), глобальный максимум, равный 5, в точке А(;2) .

2. Найти экстремумы функции L=(x1-6)2+(x2-2)2 при ограничениях

x1+x2≤8

3 x1+x2 ≤15

x1+x2 ≥1

.

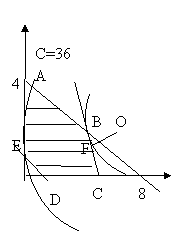Решение. ОДР – многоугольник ABCDE. Линии уровня представляют собой окружности (x1-6)2+(x2-2)2=С с центром в точке О1(6;2). Возьмём, например, С=36, видим, что максимум достигается в точке А(0;4), которая лежит на окружности наибольшего радиуса, пересекающую ОДР. L(A)=(0-6)2+(4-2)2=40. Минимум - в точке F, находящейся на пересечении прямой 3x1+x2 =15 и перпендикуляра к этой прямой, проведённого из точки О1. Т.к. угловой коэффициент равен -3, то угловой коэффициент перпендикуляра равен . Из уравнения прямой, проходящей через данную точку О1 с угловым коэффициентом , получим (x2-2)= (x1-6). Найдём координаты точки Е

х1-3х2=0

3 x1+x2 =15.

Решив систему, получаем Е(4.5; 1.5).

L (E) = (4.5-6)2+ (1.5-2)2=2.5.

Ответ: Минимум, равный 2.5 достигается в точке (4.5; 1.5), максимум, равный 40, в точке (0;4).

3. Найти экстремумы функции L=(x1-1)2+(x2-3)2

при ограничениях , .

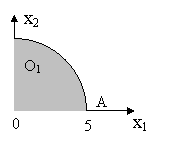Решение: ОДР является часть круга, с центром в начале координат, с радиусом 5, расположенная в I четверти. Линии уровня – это окружности с центром в точке О1 и радиуса С, т.к. (x1-1)2+(x2-3)2=С. Точка О1 – это вырожденная линия уровня, соответствующая минимальному значению С=0. глобальный максимум достигается в точке А, лежащей на пересечении ОДР с линией уровня наибольшего радиуса. При этом

L(A)=(5-1)2+(0-3)2=25.

Ответ: Минимум, равный 0, достигается в точке (1;3),

Максимум, равный 25, - в точке А(5;0).

4. Предприниматель решил выделить на расширение своего дела 150 тыс.руб. известно, что если на приобретение нового оборудования затратить х тыс. руб., а на зарплату вновь принятых работников у тыс. руб., то прирост объёма продукции составит Q=0.001x0.6·y0.4 . Как следует распределить выделенные денежные ресурсы, чтобы прирост объёма продукции был максимальным.

Решение: Целевая функция имеет вид 0.001x0.6·y0.4 →max при ограничениях x+y≤150,

.

ОДР – треугольник. Линии уровня будут иметь вид 0.001x0.6·y0.4 =С. Выразив отсюда у, получим у=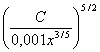. Т.к. максимум достигается в точке касания линии уровня с ОДР, то условие касания имеет вид =-1. Найдя производную, получаем =-1. Выразив х, получим х=. у==.

Ответ: Факторы х и у следует распределить в отношении 2:3.

5.Предприятие выпускает изделия А и Б, при изготовлении которых используется сырьё S1 и S2. Известны запасы bi (i=1,2) сырья, нормы его расхода на единицу изделия aij (j=1,2), оптовые цены pj на изделия и их плановая себестоимость с. Как только объём выпускаемой продукции перестаёт соответствовать оптимальному размеру предприятия, дальнейшее увеличение выпуска хj ведёт к повышению себестоимости продукции b, в первом приближении фактическая себестоимость сj описывается функцией сj= с+ схj, где сj – некоторая постоянная. Все числовые данные приведены в таблице

 Скачать реферат