Некоторые задачи оптимизации в экономике

=0 (5.7).

Поскольку в точке оптимума бюджетное ограничение выполняется как равенство, заменим на Q, получим =0. Поделив на λ, получим =-(Q-). Откуда 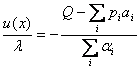. Полученное выражение подставляем в равенство (5.6)

xi=ai+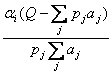 (5.8)

Т.е. вначале приобретается минимально необходимое количество продукта ai. Затем рассчитывается сумма денег, остающаяся после этого, которая распределяется пропорционально «весам» важности i. Разделив количество денег на цену pi , получаем дополнительно приобретаемое, сверх минимума, количество i- продукта и добавляем его к аi . [1] Заключение

При написании работы мною была изучена литература по данной теме. Были рассмотрены математические модели в экономике, повторены некоторые понятия функций нескольких переменных, необходимых для изучения оптимизационных задач. Также была изучена постановка задач математического программирования и методы их решения. Был рассмотрен симплексный метод, который позволяет решить любую задачу линейного программирования. Для ЗЛП была рассмотрена симметричная взаимодвойственная задача и метод её решения с использованием теорем двойственности. Для задачи нелинейного программирования был рассмотрен геометрический метод решения. А также рассмотрены задачи на условный экстремум.

В работе приводится задача потребительского выбора, решение которой сводится к решению задач на условный экстремум. Также рассмотрен частный случай задачи потребительского выбора - модель Стоуна.

Мною были решены задачи по каждому виду рассмотренных оптимизационных задач. Это ЗЛП симплексным и графическим методом, решена двойственная задача, несколько задач нелинейного программирования, задачи на условный экстремум методом подстановки и методом множителей Лагранжа, задача потребительского выбора.

Я считаю, что знание этой темы может пригодиться не только экономистам и людям, специально занимающимся этой наукой, но и ненаучным работникам, т.к. в жизни часто приходится сталкиваться с решением подобного рода задач.

Библиографический список

1. Замков, О.О. Математические методы в экономике: Учебник/ Под общ. ред. д.э.н., проф. А.В. Сидоровича/ О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных; МГУ им. Ломоносова.-3-е изд., перераб. – М.: Издательство «Дело и сервис», 2001

2. Ильин, В.А. Математический анализ/ В.А. Ильин, В.А. Садовничий, Б.Х. Сендов. – М.: Наука, 1979

3. Красс, М.С. Основы математики и её приложения в экономическом образовании: Учебник. – 3-е изд. – М.: Дело,2002

4. Кремер, Н.Ш. Высшая математика для экономистов: Учебник для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н Фридман. - М.: ЮНИТИ, 2002.

5. Кремер, Н.Ш. Исследование операций в экономике: Учебное пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ,1997.

6. Малыхин, В.И. Математика в экономике: Учебное пособие.- М.:ИНФРА - Москва, 2002.

7. Симонов, А.В. Об одном приложении производной к решению экономических задач/ А.С. Симонов, Н.Г. Игнатьев// математика в школе №9, 2001

8. Сборник задач и упражнений по высшей математике: мат. программирование: Учеб. Пособие/ А.В. Кузнецов, В.А. Сакович, Н.И. Холод; Под. общ. ред. А.В. Кузнецова – Мн.: Выш. шк., 2002

9. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под. ред. В.И. Ермакова.- М.: Инфра – Москва, 2002.

10. Сборник задач по микроэкономике. К «Курсу микроэкономики» Р.М. Нуреева/ Гл. ред. д.э.н., проф. Р.М. Нуреев. – М.: Норма, 2003

11. Фихтенгольц, Г.М. основы математического анализа. Часть 1. 4-е изд. – СПб: издательство «Лань», 2002.

12. Онегов, В.А. Исследование операций. Задачи, методы, алгоритмы. – Киров: ВГПУ, 2001.

 Скачать реферат