Модернизация подвески автомобиля ЗАЗ1102 Таврия

5240,23 ≈ 5240,16.

Aquer = √Au² + At² = √1632,91² + 682,81² = 1769,92 Н.

Силы, действующие на поршень:

К3 = 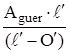– Aquer = 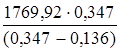–1769,92 = 1140,8 Н.

Изгибающий момент в штоке амортизатора:

Мк3 = Aquer · о′ = 1769

,92 · 0,136 = 240,71 Н м.

σдоп.= σbs / υ = 1,2 σs / υ = 1,2 · 480 / 1,5 = 384 Мпа,

т. к. υ ≥ 1,5 при кратковременных перегрузках.

Проверим выбранный в п.5.2.5 диаметр штока амортизатора по условию прочности:

.

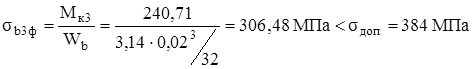Таким образом видно, что условие прочности для выбранногшо диаметра штока dmin = 20 — выполняется.

5.3.3 Силы, возникающие при торможении

Если тормозные механизмы передних колес расположены в колесе, то при коэффициенте сцепления шины с дорогой Мк = 1,25 в подвеске могут возникнуть бόльшие перегрузки, чем при движении по дороге с разбитым покрытием. Для расчета сил в рычаге подвески автомобиля в положении, соответствующем номинальной нагрузке, вычисляем продольную силу:

Lb = Мк NV = 1,25 ∙ 2885 = 3606,25 Н

и верхнее значение вертикальной силы NV'о = 4327,5 Н. Боковые силы подвески и шин можно пренебречь.

Расчет сил, возникающих при торможении, предусматривает скорость близкую к нулю. К этому следует добавить уменьшение радиуса шины в результате увеличения нагрузки. Поэтому в расчете необходимо использовать статический радиус rст. Деформация шины приводит к уменьшению плеча обкатки.

Тормозную силу LА следует считать действующей на расстоянии:

аb = Ro соs δo sin δo

над поверхностью дороги при и над ней – при отрицательном плече обкатки.

Рис. 5.8. Силы возникающие в стойке при торможении

Рассматривая силы относительно оси Z и точки А:

Σ МОZА : NV ′о · b + Вy5 (c + o) sin δo – Bx5 (c + o) cos δo = 0;

b = Ro ст + d tg δo + (c + o) sin δo; Bx5 = By5 ctg β NV ′ (Ro ст + dotg δo + (c + o) sin δo + By (c + o) sin δo – By (c + o) cos δo ctg β = 0;

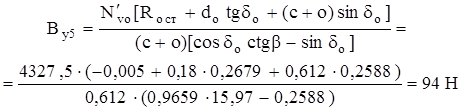
Bx5 = By5 ctg β = 94·15,97 = 1501,1 Н

Сумма моментов относительно оси Х и точки А:

Σ МОХА : NV′о · е + Вy5 · t – BZ5 (c + o) cos δo – Lb [(с + о) cos δo + d – аb] = 0;

где t = (с + о) cos δo tg ε = 0,612∙0,9659∙0,0524 = 0,031;

е = [(с +о) cos δo + dо – rст] tgε = (0,612∙0,9659+0,18–0,272)∙0,0524=0,0262.

аb =Ro стcosδosinδo = 0,005∙0,9659∙0,2588 =0,00125м.

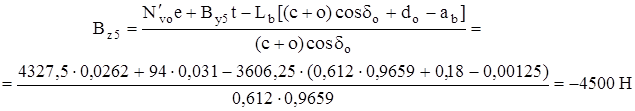
Силы в точке А:

Ах5 - Вх5 = 0; - Аy5 + Вy5 + NV ′о = 0; Аz5 - Вz5 - Lb = 0;

Ах5 = Вх5; Аy5 = Вy5 + NV′о; Аz5 = Вz5 + Lb;

Ах5 = 1501,1 Н Аy5 = 94 + 4327,5; Аz5 = -4500 +3606,25;

Аy5 = 4421,5 Н Аz5 = -893,75 Н.

Раскладываем силы на составляющие:

Ауu = Ay5 · sin υ = 4421,5 · 0,1484 = 656,15 Н.

Ayv = Ay5 · cos υ = 4421,5 · 0,9889 = 4372,42 Н.

Axs = Ax5 · sin æ = 1501,1 · 0,937 = 1406,53 Н.

Axt = Ax5 · cos æ = 1501,1 · 0,3494 = 524,48 Н.

Azs = Az5 · cos æ = - 893,75 · 0,3494 = - 312,28 Н.

Azt = Az5 · sin æ = - 893,75 · 0,937 = - 837,44 Н.

As = Azs + Axs = - 312,28 + 1406,53 = 1094,25 Н.

At = Axt – Azt = 524,48 – (- 837,44) = 1362,27 Н.

Asu = As · cos υ = 1094,25 · 0,9889 = 1082,06 Н.

Asv = As · sin υ = 1094,25 · 0,1484 = 162,38 Н.

F1 = Ayv + Asv = 4372,42 + 162,38 = 4534,8 Н.

Au = Asu – Ayu = 1082,06 – 656,15 = 425,91 Н.

Осуществляем проверку разложения сил:

√Ах5² + Ау5² + Аz5² = √A u² + At² + F1² ;

√1501,1² + 4421,5² + (- 893,75)² = √425,91² +1362,27² + 4534,8² ;

4754,13≈4754,11

Aquer = √Au² + At² = √425,91² + 1362,27² = 1427,3 Н.

Сила в направляющей втулке штока амортизатора:

С5 = Аquer · ℓ′ / (ℓ′ – о′) = 1427,3 ∙ 0,347 / (0,347 – 0,136) = 2347,27 Н

Сила, действующая на поршень:

К5 = С5 – Аquer = 2347,27 – 1427,3 = 919,97 Н

Изгибающий момент в штоке амортизаторной стойки:

Мк5 = Аquer · о′ = 1427,3 · 0,136 = 194,11 Н м;

Т. к. изгибающий момент для этого случая меньше момента для случая движения по разбитой дороге (Мк5 < Мк3), то заведомо можно сказать, что условие прочности для данного случая выполняется.

По-прежнему фиксируем пока минимальный диаметр штока dmin = 20 мм.

5.3.4 Силы, возникающие в подвеске при

преодолении железнодорожного переезда

При расчете максимальных вертикальных нагрузок следует установить колесо в крайнее верхнее положение, сместив его на величину хода f1 (рис. 5.9). Это необходимо для определения изменившихся углов (с индексом 2) ε2 δ2, β2, а также изменившегося плеча обкатки Ro2. При расчете на прочность используется положение автомобиля при допустимой полной загрузке. Используем действующие в пятне контакта силы:

NV ′2 = NV 2 – (U2 / 2) и S1 = µF1 NV.

NV′2 = 2,6∙2885 – 288,5 = 7212,5 Н.

S1 = 981 Н.

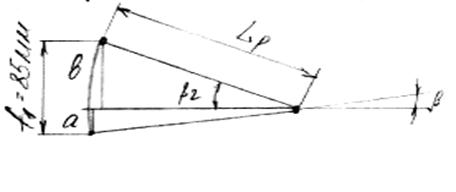
Рис. 5.9 Изменение положения рычага при преодолении железнодорожного переезда

Определяем угол β2:

sin β = a / Lp; sin β2 = b / Lp;

b = 65 – а = 65 - Lр sin β;

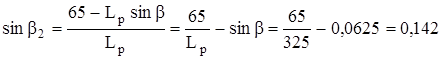
β2 = 8°08′.

Угол δ2 определяем графически через соотношение изменившегося расстояния между точками А и В и его проекцией на ось ОУ:

соs δ2 = 0,528 / 0,551 = 0,9583; δ2 ≈ 16°36′.

При ходе сжатия подвески существующее расстояние о (между направляющей с и точкой А в крыле) уменьшается до:

о′2 = о′ - f1 / ix = 0,136 – 0,065 / 1,0112 = 0,072 м.

Изменившийся угол ε2:

ε2 ≈ 3°22′.

Изменившееся плечо обкатки:

Ro2 = - d tg δ2 + к = -0,203∙0,2934 + 0,025 = -0,035 м;

где к = 0,025 м.

аL2 = Ro2 · sin δ2√(1 + tg²ε2) (1 + tg²ε2 + tg² δ2) + rд sin (δ2 + γ2) sin δ2 ;

где γ2 = δ2 – δо = 16º36′ – 15° = 1°36′

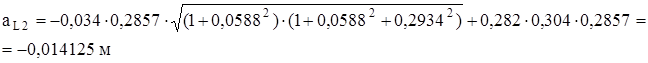
nS2 = rд sin²ε2 = 0,282 · 0,0587² = 0,001 м

 Скачать реферат