Модернизация подвески автомобиля ЗАЗ1102 Таврия

По приведенному на рис. 5.10 виду сзади, используя зависимость Вх2 = Ву2 сtg β2, составляем уравнение моментов относительно оси ОZ и точки А:

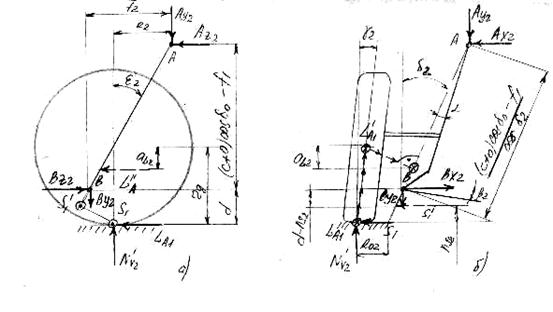
Рис. 5.10 Виды сбоку (а) и сзади (б).

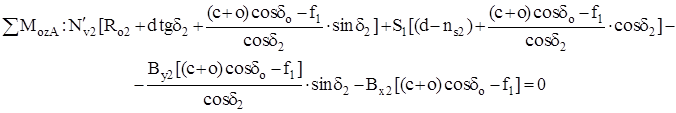
Bx2= Ву2 сtg β2 = 453,71 · 8,105 = 3677,32 Н.

Сумма моментов относительно оси ОХ и точки А:

Σ МОХА : NV′2 · е2+LA1[(с+о)cosδo– f1 + d – (rд – aL2)] – By2 · f2 – Bz2·[(с + о)cos δo – – f1] = 0;

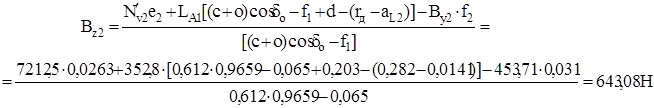
Где е2=[(с+о)cosδo–f1+d–rд]tgε2=(0,612∙0,9659–0,065+0,203–0,282)∙0,0588=0,0263;

f2 = [(с + о)cosδo– f1] tg ε2=(0,612∙0,9659–0,065)∙0,0588= 0,031.

В точке А действуют взаимно перпендикулярные силы:

- Ах2 + Вх2 - S1= 0; - Аy2 + NV′2 - Вy2 = 0; - Аz2 + Вz2 - LА1 = 0;

Ах2 = Вх2 - S1; Аy2 = NV′2 - Вy2; Аz2 = Вz2 – LА1;

Ах2 = 3677,32 – 981; Аy2 = 7212,5 – 453,71; Аz2 = 643,08 – 352,8;

Ах2 = 2696,32 Н Аy2 = 6758,79 Н Аz2 = 290,28 Н

Раскладываем эти силы в направлении оси амортизатора и перпендикулярно ей аналогично предшествующим случаям.

Определяем пространственный угол υ2:

tg υ2 = √tg² (δ2 – α) + tg² ε2

tg υ2 = √tg² 8°21′ + tg² 3°22′ = √0,1468² + 0,0588² = 0,15814.

υ ≈ 8°59′.

Определяем пространственный угол æ2:

tg æ2 = tg (δ2 – α) / tg ε2 = 0,1468 / 0,0588 = 2,4966

æ = 68°10′.

Аyu = Аy2 · sin υ2 = 6758,79 · 0,1561 = 1055,05 Н

Аyv = Аy2 · cos υ2 = 6758,79 · 0,9877 = 6675,66 Н.

Ахs = Ах2 · sin æ2 = 2696,32 · 0,9283 = 2503 Н

Ахt = Ах2 · cos æ2 = 2696,32 · 0,3719 = 1002,76 Н

Аzs = Аz2 · cos æ2 = 290,28 · 0,3719 = 107,96 Н

Аzt = Аz2 · sin æ2 = 290,28 · 0,9283 = 269,47 Н

Аs = Аzs + Ахs = 107,96 + 2503 = 2610,96 Н

Аt = Ахt – Аzt = 1002,76 – 269,47 = 733,29 Н

Asu = As · cos υ2 = 2610,96 · 0,9877 = 2578,85 Н.

Asv = As · sin υ2 = 2610,96 · 0,1561 = 407,57 Н.

F1 = Ayv + Asv = 6675,66 + 407,57 = 7083,23 Н.

Au = Asu – Ayu = 2578,85 – 1055,05 = 1523,8 Н.

Осуществляем проверку разложения сил:

√Ах2² + Ау2² + Аz2² = √Au² + At² + F1² ;

√2696,32² + 6758,79² + 290,28² = √1523,8² + 733,29² + 7083,23² ;

7282,56 ≈ 7282,3.

Aquer = √Au² + At² = √1523,8² + 733,29² = 1691,06 Н.

Сила в направляющей втулке амортиизаторной стойки:

с2 = Aquer ℓ′ / (ℓ′2 - о′2) = 1691,06 · 0,347 / (0,347 – 0,072) = 2133,81 Н.

Сила, действующая на поршень:

К2 = с2 - Aquer = 2133,81 – 1691,06 = 442,75 Н.

Изгибающий момент в штоке амортизатора:

Мк2 = Aquer · о′2 = 1691,06 · 0,072 = 121,76 Н м.

Т. к. изгибающий момент для этого случая меньше моментов прочности для случая максимальной вертикальной нагрузки выполняется.

Минимальный диаметр штока dmin = 20 мм.

5.3.5 Силы, действующие при полном ходе отбоя колеса

Чтобы учесть все напряжения изгиба в штоке амортизатора, следует рассматривать действия боковых сил от поперечных составляющих неровностей дороги при крайнем нижнем положении колеса (рис. 5.11). При этом ограничитель хода отбоя, закрепленный на штоке амортизатора, упирается в направляющую втулку штока в зоне точки С.

Определяем угол β4:

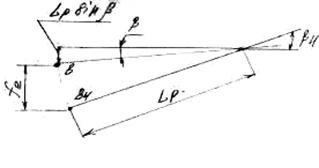
Рис. 5.11 Изменение положения рычага при полном ходе отбоя

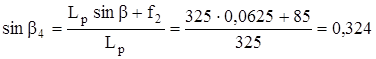; β4=19º

Определение углов наклона оси поворота δ4 и развала колеса γ4.

В этом случае не будем пренебрегать изменением угла α между осью поворота и осью амортизатора, как это было сделано в случае максимальной вертикальной нагрузки (случай 2 п.5.3.4) из-за ничтожного его изменения в сравнении с изменением угла δo → δ2. Так как очень сложно учесть все факторы, влияющие на изменение развала γ, то единственными критериями оценки изменения угла α можно считать кратчайшее расстояние от центра шаровой опоры до оси амортизатора и угол δo – α = 8° между осью колеса и осью амортизатора, которые неизменны при любом положении подвески.

Угол δ4 определяем графически с учетом масштаба по рис. 5.12 через соотношение:

соs δ4 = j/q = 0,671 /0,685 = 0,9796,

что соответствует δ4 = 11°36′.

Аналогично определяем угол α4 :

sinα4= t/q= 0,045 / 0,685 = 0,0571, α4 ≈ 3°44′.

Находим развал при полном ходе отбоя:

g4=(d4-a4)-(d0-a)=(11°36¢-3°44¢)-(15°-7°)= -0,08¢.

Составляем уравнение моментов относительно т.А:

SМА:S1[d+fm+(c+o)cosd0+f2]+BX4[(c+o)cos d0+f2]-

-BY4[(c+o)cos d0+f2]sin d4/cosd4=0

Учитывая, что BX4=BY4∙Ctg b4 и sin d4/cos d4=tg d4:

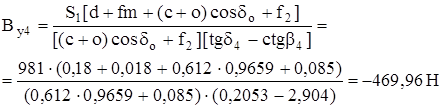
BX4= -469,96∙2,904= -1364,76 H.

Силы в точке А:

-Aх4+Bх4+S1=0; -Aу4+Bу4=0;

Aх4=Bх4+S1; Aу4=Bу4;

Aх4= -1364,76+981= -383,76 H; Aу4= -469,96 H.

Aуt=Aу4∙cos (d4-a4)= -469,96∙0,9979= -468,97 H.

Aуs=Aу4∙sin (d4-a4)= -469,96∙0,0651= -30,59 H.

Aхt=Aх4∙sin (d4-a4)= -383,76∙0,0651= -24,98 H.

Aхs=Aх4∙cos(d4-a4)= -383,76∙0,9979= -382,95 H.

As=Aхs–Aуs= -382,95–(-30,59)= -352,36 H.

At=Aуt+Aхt= -468,97+(-24,98)= -493,95 H.

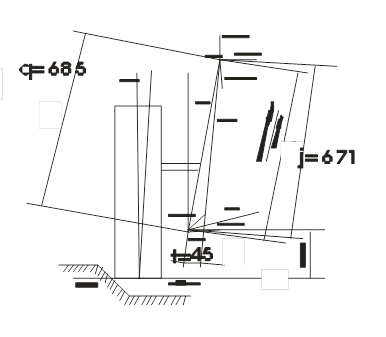
Рис. 5.12 Схема сил в подвеске при полном ходе отбоя.

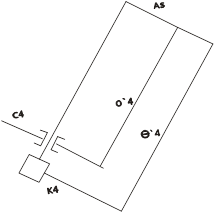
Рис. 5.13 Силы действующие на шток амортизатора при полном ходе отбоя.

Проверка:

606,74»606,75.

O¢4=O¢+f2/ix=0,136+0,085/1,0112=0,2186 м.

Сила в направляющей втулке амортизаторной стойки:

C4=AS∙l¢/(l¢-O¢4)= -352,36∙0,347/(0,347- -0,2186) = -952,25 H.

Сила, действующая на поршень:

K4=C4-AS= -952,25–(-352,36)= -599,89 H.

Момент, изгибающий шток:

MK4=AS∙O¢4= -352,36∙0,2186= -77,03 Hм.

Т. к. изгибающий момент для этого случая меньше всех рассчитанных раньше моментов, то условие прочности выполняется.

Окончательно имеем диаметр штока амортизаторной стойки d=20 mm.

6 Подрессоривание передней оси

 Скачать реферат