Элементы математического кружка на уроках математики в 5-6 классах

Много заданий на смекалку:

2) В числе 92574063 зачеркни три цифры так, чтобы оставшиеся пять цифр в той же последовательности образовали:

- Возможно большее число;

- Возможно меньшее число;

Некоторые задания выполнены в виде игры. Например:

3) Игра "Кто больше"?

1.Какая фигура изображена на

рисунке? Измерьте его стороны, углы, диагонали и перечислите как можно больше свойств.

2.Сколькими способами можно пройти из А в Д ? Перечислите все пути.

3. Сколько на рисунке прямых, острых, тупых углов? Назовите все пары вертикальных и смежных углов.

При анализе учебника математика – 5, авторы: И.И.Зубаревой, А.Г.Мордковича, мы не обнаружили большое количество развивающих заданий. В основном они все похожи на задания из учебника математика-5, авторы: Г.В. Дорофеев, Л.Г.Петерсон. Многие задания переделаны на современный лад. Например: Антон забыл кодовый номер своей банковской магнитной карты, но помнил, что он состоит из четырех цифр и сумма двух первых цифр = 15, а двух вторых – 16. Запишите все возможные варианты кодового номера его магнитной карты. Можно ли утверждать, что он наверняка сможет воспользоваться картой, если она запрограммирована так, что ошибиться можно не более четырех раз ?

Мало заданий повышенной сложности, которые носят наглядный характер. В основном все задачи логические.

В учебнике математика - 6 , авторы: Г.В.Дорофеева, Н.Ф.Шарыгина, задания похожи на все предыдущие. Многие напоминают задания из рабочей тетради.

1) Заполните пропуски в предложениях:

а) Чтобы найти половину некоторого числа, нужно это число разделить на или умножить на _.

б) Чтобы найти десятую часть некоторого числа, нужно это число разделить на _ или умножить на .

Много геометрических заданий.

2)

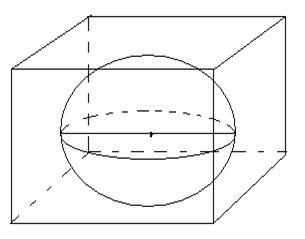
Шар поместили в куб так, что он касается всех граней куба. Ребро куба = 6 см. Чему равен диаметр шара?

Так же есть древняя китайская головоломка – Танграм.

3) У кошек 2*4 лапы, 2*2 уха, 2 носа. Продолжите запись:

У кошек 4*4 лапы, ……, уха,……носа.

У 15 кошек … лап, … ушей, … носов.

У п кошек…… лап, …… ушей, … носов.

4) Придумайте по три примера достоверных, невозможных и случайных событий.

Анализ учебника математика – 6, под. ред. Г.В. Дорофеев, Л.Г.Петерсон, показал, что в нем содержится большое количество заданий направленных на развитие логического мышления, внимания, памяти и интереса к предмету.

1)Замени буквы цифрами ( одинаковым буквам соответствуют одинаковые цифры):

а) ЛЕТО +ЛЕТО = ПОЛЁТ

б) ПЧЕЛКА * 7 = ЖЖЖЖЖЖ

2) Шифр устроен следующим образом: каждой цифре сопоставлено 3 буквы, а знаку * - 2 буквы и пробел, как указано в таблице:

0 1 2 3 4 5 6 7 8 9 *

а г ж й м п т х ш ы ю

б д з к н р у ц щ ь я

в е и л о с ф ч ъ э

Попробуй расшифровать следующую запись:

61551491*2*6561*051*51516566

Следующие задания логического характера учат школьников умению рассуждать, формируют математический стиль мышления.

3) У мальчика столько же сестер, сколько братьев, а у его сестры вдвое меньше сестер, чем братьев. Сколько в этой семье братьев и сестер?

4) В двух пачках было 30 тетрадей. Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке ?

5) Нарисуй недостающую фигуру. Задачи на исключение лишнего:

6) Найдите лишнее слово и объясни, почему оно лишнее. Если возможно укажи несколько вариантов решения:

а) капитан, феномен, огород, работа, оператор,

Б) одокрилк, крочевс, шаркаадн, аакчобб, ципат,

Такие задачи способствуют формированию умения поиска задачи, интуиции, требуют знания теории и нешаблонного подхода к решению задач.

Наглядные задания следующего плана:

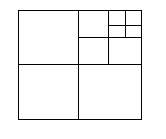
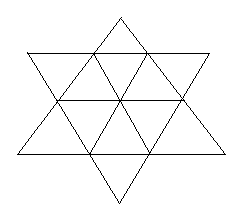
7) Сколько изображено на рисунке:

а) квадратов. б) треугольников.

Есть много ребусов.

8)

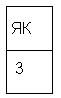
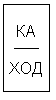
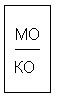
9) Много или мало составляют:

а) 3 волоса на голове и в супе ?

б) прибавка в 1 г. Для муравья и для слона ?

Придумайте свои примеры, когда одно и то же значение величины даёт разную качественную оценку некоторой ситуации.

10) Сделай один ступенчатый разрез "ступеньки" так, чтобы из двух получившихся частей можно сложить квадрат.

11) Математические софизмы. (логически неправильные рассуждения, выданное за правильное).

" Дважды 2 – пять!"

Возьмем верное равенство: 28+8-36=35+10-45

В каждой части этого равенства вынесем за скобки общий множитель: 4( 7+2-9) = 5 ( 7+2-9). Теперь решив обе части равенства на общий множитель? ( 7+2-9), получим, что 4=5, то есть 2*2 = 5. Где ошибка ?

12) Слово "СЕНО" имеет горизонтальную ось симметрии, а слово "ШАЛАШ" - вертикальную. Также оно является палиндромом – при чтении его с права налево получается тоже самое слово. Палиндромом является предложение: " Аргентина МАНИТ НЕГРА". Придумай свои примеры симметричных палиндромов и слов.

Такие задания развивают логическое мышление, заставляют школьников размышлять нестандартно.

При анализе учебника математика – 6 под. ред. Э.Р.Нурка и А.Э. Тельгмаа интересных заданий, которые были бы направлены на развитие логического мышления и интереса к предмету не обнаружено.

Таким образом, можно сделать вывод, что не многие учебники содержат задания направленные не только на отработку необходимых, умений и навыков, а так же формирование пространственного и логического мышления, математического стиля рассуждений, развитие лингвистических способностей детей, которые приводят к умению мыслить. Наличием таких заданий на первый план можно выделить следующие учебники: 1) "Математика 5-6" под. ред. Г.В. Дорофеев, Л.Г.Петерсон. 2)"Математика 6 кл". общеобр. учреждений/Г.В.Дорофеев, Н.Ф.Шарыгин. 3) "Математика 5 кл". общеобр. учреждений/И.И. Зубарева, А.Г.Мордкович– 2-е изд.-М.: Мнемозина, 2003 г.-293 с.

4) "Математика 5 кл." общеобр. учреждений/Н.Я. Виленкин, В.И.Жохов, А.С.Чесноков, С.И. Шварцбурд.

Психолого-педагогическая характеристика учащихся 5-6 классов

Возраст учащихся 5-6 классов находится на границе возраста младшего школьника (от 7 до 11 лет) и подросткового возраста ( от 11 до 15 лет).

Младший школьный возраст – начало школьной жизни. Вступая в него, ребёнок приобретает внутреннюю позицию школьника, учебную мотивацию. Учение для него – значимая деятельность. В школе он приобретает не только новые знания и умения, но и определенный социальный статус. Меняются интересы, ценности ребенка, весь уклад его жизни. По мнению Л.И.Божовича, в этот период происходит кризис семи лет – период рождения социального "Я" ребёнка. Изменение самосознания приводит к переоценке ценностей. То, что было значимо раньше, становиться второстепенным, старые интересы, мотивы теряют свою побудительную силу. Всё, что имеет отношение к учебной деятельности (в первую очередь отметки), оказывается ценным то, что связано с игрой, - менее важным. Что касается учебной деятельности, то в неё ребенок входит как наиболее значимую для него, а исходит благодаря изменению социальной ситуации развития ребёнка, ориентирующегося на общественную ценность того, что он делает. Утрата интереса к игре и становление учебных мотивов по мнению И.Ю. Кулагиной, связаны с особенностями развития самой игровой деятельности. Для младшего школьника характерны игры по правилам, выигрывает тот, кто лучше освоил игру. В игровой мотивации смещается с процесса на результат, развивается мотивация достижения. Сам ход развития детской игры приводит к тому, что игровая мотивация постепенно уступает место учебной, при которой действия выполняются ради конкретных заданий и умений, что даёт возможность получить одобрение, признание взрослых и сверстников, особый статус.