Элементы математического кружка на уроках математики в 5-6 классах

Следующий параграф 3: Умножение и деление натуральных чисел.

В начале изучения этой темы можно предложить ученикам необычный способ умножения. С начало они сами должны решить эти примеры, а затем учитель показывает необычный способ умножения.

1) Вычислите: а) 13 × 64 = ?

Решение: Произведение 13 × 64 не изменится, если первый множитель умножить на 2, а второй разделить н

а 2, т.е.

13 × 64 = 26×32= 52×16 = 104×8 = 208×4= 416×2 =832

б) 24×17 =?

В этом случае можно поступить немного иначе:

24×17= 24×16+24, 24×16= 48×8=96×4=192×2=384, тогда в итоге получается 24×17= 384+24=408

Можно задать необязательную домашнюю работу: Вычислить а) 48×15

б) 36×12

2) Еще одно занимательное умножение, называется "Парад чисел".

а) 11×11=121

111×111=12321

1111×1111=1234321

11111×11111=123454321

………………………….

111111111×111111111= ?

А над этой строчкой они должны будут подумать сами и сделать вывод.

б) Аналогично и в этом пункте.

1×9+2=11

12×9+3=111

123×9+4=1111

………………

123456×9+7=?

3) Пять мальчиков, встретившись, обменялись рукопожатиями. Сколькими?

4) К трёхзначному числу слева приписали 3, и оно увеличилось в 9 раз. Какое это число?

Следующий параграф: Площади и объёмы.

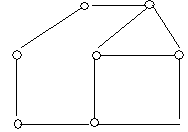
1) Из спичек построен "дом". Переложите две спички так, чтобы он перевернулся другой стороной.

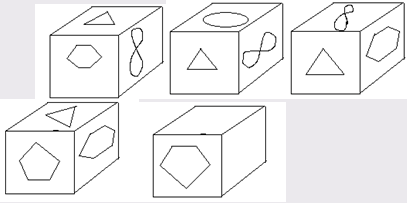
3) Кубик последовательно перекатывают с грани на грань. Какие фигуры должны располагаться на верхней и правой боковой гранях последнего изображения кубика? Нарисуйте их.

3) На рёбра непрозрачного куба напаяна проволока.

Как проходит проволока, показано на изображении куба. Нанесите её на виды куба спереди , сверху и слева.

а)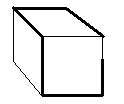

Следующий параграф: 5. Доли. Обыкновенные дроби. Сложение и вычитание дробей с одинаковыми знаменателями.

1) Как девять деревьев посадить в 8 рядов, что бы в каждом ряду было по три дерева?

2) Интересные свойства чисел.

Можно показать ребятам некоторые интересные факты относительно умножения на 9:

1×9= 09 90= 9×10

2×9= 18 81= 9×9

3×9= 27 72= 9×8

4×9= 36 63= 9×7

5×9 =45 54= 9×6

Как видно, выделенные числа – зеркальные отражения соседних.

3) Разрежьте квадрат на 4 равные части. Затем такой же – на 16 равных частей. Получилось? А теперь точно такой же квадрат – на 17 равных частей.

4) Можно ученикам задать подготовить доклад на тему: Происхождение дробей.

5) Имеются два сосуда вместимостью 3 и 5 л. Как с помощью таких сосудов налить из водопроводного крана 4 л.?

6) Сравните значения выражений, не выполняя сложение.

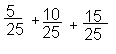
7) Когда велосипедист проехал 2/3 пути, лопнула шина. На остальной путь пешком он затратил вдвое больше времени, чем на велосипедную езду. Во сколько раз велосипедист ехал быстрее, чем чисел?

8) (На повторение). Игра на внимание. На доске написан "столбик" чисел. Быстро и вслух суммируйте число за числом:

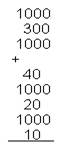
9) Помните, у К.И.Чуковского:

У меня зазвонил телефон.

- Кто говорит?

- Слон.

………………

А потом зазвонил Крокодил…

А потом зазвонили Зайчики…

А потом зазвонили Мартышки…

А потом зазвонил Медведь…

А потом зазвонили Цапли…

Итак, у Слона, Крокодила, Зайчат, Мартышек, Медведя, Цапель и у автора установлены телефоны. Каждые 2 телефонные аппарата соединены проводом. Как сосчитать, сколько для этого понадобиться проводов.

Следующий параграф: 6 Десятичные дроби. Алгебраические операции с десятичными дробями.

1) Имеются двухчашечные весы и гири массой 1,2,4,8,16 г. На одну чашу весов кладут груз, на другую можно класть гири. Докажите, что весы можно уравновесить, если масса груза равна: а) 13, 19, 23 и 31 г. б) любому целому числу граммов от 1 до 31 включительно.

2) Группа туристов хочет попасть из деревни А в деревню В. За какое наименьшее время это возможно?

3) Как из трёх спичек сделать четыре, не ломая их?

4) Из 12 спичек сложено имя "Толя".

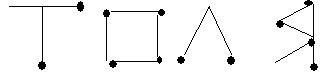
Переложите одну спичку так, чтобы получилось женское имя.

Задачи на нахождение среднего арифметического и задачи на проценты.

1) Средний возраст 11 футболистов команды 22 года. Во время игры один из игроков получил травму и ушёл с поля. Средний возраст оставшихся игроков стал 21 год. Сколько лет футболисту ушедшему с поля?

2) Из теста можно сделать 20 одинаковых калачей или 25 одинаковых булочек. Какова масса всего тела, если на один калач идёт на 10 г. дольше, чем на одну булочку?

3) Можно задать ребятам, подготовить доклад на тему: Проценты. Как и где проценты применяются в жизни.

4) Дед рассказывал своим внучатам: "В комнате было 5 стульев, на них сидели 4 матери, 4 дочки, 3 бабушки, 2 прабабушки и одна прапрабабушка. При этом каждая женщина сидела на отдельном стуле." "Это не возможно", - Возразили внучата. "Я сам видел", - ответил дед. Возможно ли это?

5) Эту задачу можно задать школьникам на дом как необязательное домашнее задание. А на следующем уроке проверить всем вместе ответ и у кого он будет более полным, поставить положительную оценку.

Цена входного билета на стадион была 1 р. 80 коп. После снижения входной платы число зрителей увеличилось на 50 %, а выручка выросла на 25 %. Сколько стал стоить билет после снижения?

Задания на повторение. Во время повторения курса пятого класса, можно нестандартные задания задавать школьникам чаще. Некоторой список заданий описан ниже.

1) Постройте отрезок АС так, чтобы САВ был прямым(см. на рис.)

2) Постройте АВС, равный 45 . Постройте квадрат со стороной ВС.

3)Начертите произвольный пятиугольник и проведите все диагонали из какой – нибудь его вершины. Сколько всего диагоналей у пятиугольника?

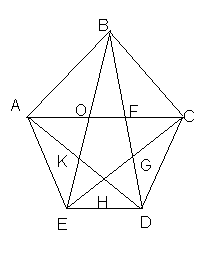
С помощью транспортира измерьте и сравните все получившиеся углы.