Элементы математического кружка на уроках математики в 5-6 классах

Так же в этот период от школьной успеваемости, оценки ребенка как хорошего или плохого ученика непосредственно зависит развитие его личности. А.Н.Леонтьев считает, что мотивационная сфера это ядро личности. Главное место среди разнообразных социальных мотивов учения занимает мотив получения высоких отметок. Высокие отметки – источник эмоционального благополучия, предмет гордости. Другие социаль

ные мотивы учения – дом, ответственность, необходимость получить образование. Большинству младших школьников так же присуще познавательные интересы не слишком высокого уровня. Хорошо успевающие дети ситуативно, на разных уроках, при изучении разного учебного материала дают всплески интереса, подъём интеллектуальной активности.

Важный аспект познавательной мотивации – учебно-познавательные мотивы, но даже среди хороших учеников крайне мало детей имеющих такие мотивы. Развиваются такие мотивации как: мотивация достижения успеха, престижная мотивация, у неуспевающих детей – компенсаторная мотивация. Центральной в этом возрасте является проблема школьной успеваемости, оценка результатов учебной работы детей. Это влияет на становление самооценки. У неуспевающих и некоторых хорошо успевающих учеников складывается завышенная самооценка. У неуспевающих и крайне слабых учеников систематические неудачи и низкие оценки снижают их уверенность в себе, в своих возможностях. По данным исследования М.А.Боцмановой и А.В.Захаровой, описывая более популярные качества у сверстников, учащиеся 5-6 классов указывают в первую очередь на ум и знания. Для развития у детей адекватной самооценки и чувства компетентности необходимо создание в классе атмосферы психологического комфорта и поддержки.

Учащиеся шестых классов (и некоторые пятиклассники) начинают входить в подростковый возраст. Поэтому далее будет описано начало подросткового возраста.

После относительно спокойного младшего школьного возраста подростковый кажется бурным и сложным. Главной особенностью этого возраста является личностная нестабильность. Особенно можно выделить формирующиеся у него чувства взрослости и "Я - концепция". Чувство взрослости – особая форма самосознания. Оно проявляется в стремлении к самостоятельности, желании оградить какие –то стороны своей жизни от вмешательства родителей. "Я - концепция" - система внутренне согласованных представлений о себе, образование "Я". В 11-12 лет возникает интерес к своему внутреннему миру, а затем происходит постепенное усложнение и углубление самопознание.

Что касается развития психических функций в этом возрасте, продолжает развиваться теоретическое рефлексивное мышление. Приобретенные в младшем школьном возрасте операции становятся формально – логическими операциями. Подросток, абсорбируясь от конкретного, наглядного материала, рассуждает в словесном плане. На основе общих посылок он строит гипотезы и проверяет их. Так же он приобретает взрослую логику, происходит дальнейшая интеллектуализация восприятие и памяти, воображения. Появляется подростковая дружба и объединение в неформальные группы. Возникают яркие, изменчивые увлечения. Появляется склонность к самоанализу.

Учитывая психолого-педагогические особенности возраста учеников 5-6 классов, а так же основываясь на особенности учебного материала в этих классах, в следующей главе будет составлено примерное планирование с добавлением заданий из математического кружка. Которое может пригодиться учителям в работе с детьми, а так же поможет сделать урок нестандартным, интересным и увлекательным.

Примерное планирование учебного материала по математики в 5 классе, содержащие нестандартные задания из математического кружка

Учителю, преподающему в 5-6 классах, можно развивать логическое мышление учащихся придерживаясь следующих пунктов:

1.Выбранные задания должны быть посильными для детей.

2.Задания, отобранные для одного урока, должны быть разнообразными для воздействия на различные компоненты мышления;

3.Если ученики при выполнении задания не справляются с ним, то целесообразно оставить его на обдумывание до следующего урока.

4.Можно задавать ученикам необязательное домашнее задание по составлению аналогичных задач.

Первым большим блоком в изучении математики в 5 классе, являются: Натуральные числа и шкалы.

Изучив содержание данного учебника, мы решили, что для развития логического мышления, и для того чтобы разнообразить процесс обучения можно воспользоваться заданиями которые будут изложены ниже. Эти задания чаще используются на занятиях математического кружка.

1) Математическая игра "Не собьюсь". Учитель вызывает одного ученика к доске и задаёт ему вопрос:

- До какого числа ты умеешь считать?

Ученик отвечает.

Правила игры: нужно считать по определённому правилу. Ученики не должны называть "три", числа, делящиеся на три, и в название которых входит цифра 3. (Например 13).Вместо этих чисел он должен говорить: "Не собьюсь". После первой ошибки, выходит другой ученик.

Такую игру можно использовать на первых уроках математики, вместо устного счета.

2) Так же ученикам можно задать темы для докладов:

- "Цифры у разных народов".

- "Счет у первобытных людей".

3) Сколько отрезков с отмеченными концами можно найти на этом рисунке?

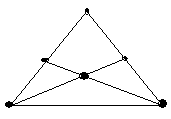
4) Такое задание можно задать детям на дом как необязательное, а на следующем уроке со всеми вместе проверить. А тому, кто точнее всех ответит поставить положительную оценку.

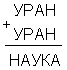
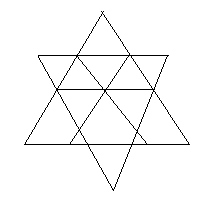
5) Сколько треугольников изображено на рисунке?

6) На рисунке виде отрезков изображён рост пяти мальчиков. Какое из следующих утверждений неверно?

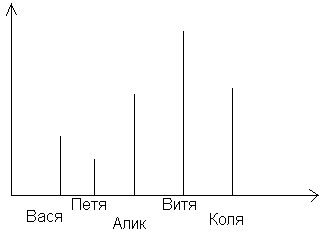
А – Витя – самый высокий.

Б – Алик и Коля одинакового роста.

В – Вася – самый маленький.

Г – Петя – ниже всех остальных.

7) Какие из линий изображённых на рисунке, можно начертить одним росчерком, а какие нельзя?

а)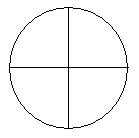 б) в)

Следующий идёт параграф: Сложение и вычитание натуральных чисел.

1) Можно решить логическую задачу следующего плана: Тетрадб, ручка, карандаш, книга стоят 37 руб. Тетрадь и карандаш вместе стоят 5 руб. Сколько стоит каждая вещь в отдельности?

2) На коврике изображено семь роз. Требуется тремя прямыми линиями разрезать коврик на семь частей, каждая из которых содержала бы по одной розе:

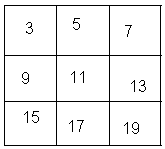
3) В клетках квадрата представьте числа так, что бы по любой вертикали, горизонтали и диагонали их суммы были равны между собой: