Модели массвого обслуживания

Поскольку процесс однороден во времени, величина Pin (h) при h > 0 определяет не только вероятность перехода на интервале (0, h), но и вероятность перехода на интервале (Т, Т+h) при произвольном значении Т, т. е. представляет собой вероятность того,что в момент Т+ h в системе будет находиться п требов

аний при условии, что в момент Т в данной системе находилось i требований. Нами постулируется, что вероятности Pin (Т) удовлетворяют известным уравнениям Колмогорова — Чэпмена для однородныхво времени марковских процессов.

Эти уравнения имеют следующий вид:

при любых значениях i и т. Соотношения (2) эквивалентны утверждению, что вероятность обнаружения в системе п требований в момент Т + h при условии, что в системе было i требований в момент Т, можно определить путем сложения произведений совместных вероятностей наличия в системе т требований в момент Т при наличии в ней i требований в момент 0 и вероятностей наличия в системе п требований в момент T+h, при условии, что в момент Т в системе находилось т требований. Так называемое марковское свойство процесса просто означает, что действительно существенной информацией для описания состояния системы в момент Т является лишь информация о количестве требований, находящихся в системе в этот момент (это число мы обозначили через т), а информация о всей предыстории протекания процесса до момента Т оказывается совершенно несущественной . В этом смысле система ≪не обладает памятью≫ (или, как иногда говорят, является системой ≪без последействия≫) и, следовательно, условие (2) является нетривиальным.

Процесс рождения и гибели является частным случаем дискретного марковского процесса, определяемого уравнением (2). Предположим, что в течение очень малого интервала времени (Т, Т+h), причем h > 0, количество поступивших в систему требований, так же как и количество требований, обслуженных системой, не превышает единицы (т. е. равняется либо нулю, либо единице). Для этого случая мы получим

Соотношение (6) является уже не приближенным, а точным, так как при h → 0 члены, опущенные нами в (5), в процессе указанного предельного перехода обращаются в нуль. Уравнение (6) позволяет также описать случай, когда п = 0; для этого достаточно положить

λ-1= 0 и μ0 = 0. Итак, (6) представляет собой систему уравнений для п =0О, 1, 2, . . . при начальном количестве требований в системе, равном i.

Термин опережающие уравнения отражает то обстоятельство, что при их выводе рассматривалось положительное приращение времени в пределах интервала (Т, T+h), где h > 0, а в качестве приближенных формул для вероятностей переходов были использованы соотношения (3) и (4). Можно вывести также ≪запаздывающие уравнения≫, рассматривая переходы на интервале (Т+ h, Т) при h > 0 [или, что то же самое, на интервале (Т, T+h) при h < 0] и используя аналоги соотношений (3) и (4) для Pim (h), построенные применительно к данному случаю. В получаемых таким путем дифференциальных уравнениях значение п в момент Т считается заданным, a i (т. е. количество требований, находящихся в системе в момент 0) варьируется, принимая значения i = 0, 1, 2,

Систематизация полученных ранее результатов. Попытаемся теперь показать, что из уравнений (6) вытекают (как частные случаи) уравнения для ряда моделей, анализ которых проведен нами в предыдущих разделах данной главы. Рассмотрим модель чистого рождения с пуассоновским входным потоком . Для чистого рождения λn = λ,, а μn = 0 при любых значениях п. В предположении, что в момент 0 i = 0, уравнение (6) переходит в уравнение

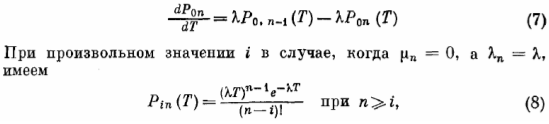
что согласуется с приведенными до этого формулами (10) и (XI) для i = 0.

Примеры.

Попытаемся теперь продемонстрировать возможности, заложенные в уравнениях для процессов рождения и гибели.

Пример 1. Предположим, что поток требований является пуассоновским с параметром λ, причем будем считать, что каждое требование обслуживает себя в соответствии с экспоненциальным распределением длительностей обслуживания с параметром μ. (Такую систему можно квалифицировать как систему с бесконечно большим количеством обслуживающих приборов и представить символически в виде М/М/∞. Таким образом, λn = λ,, а μn = μn.

Следовательно,

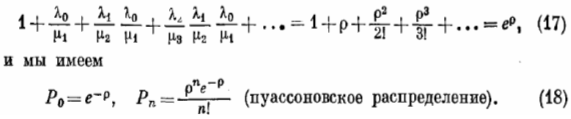
Пример 2. Пусть имеется один прибор, характеризующийся экспоненциальным распределением длительностей обслуживания, т. е. μn = μ (п ≥1). Однако допустим, что наблюдаются отказы требований присоединиться к очереди, причем наблюдается следующая закономерность: λn = λ/(n+1). Нетрудно убедиться, что при сформулированных выше предположениях мы также придем к формулам (17) и (18).

Пример 3. До сих пор нами анализировались модели, в которых предполагалось, что источник требований обслуживания неисчерпаем. Рассмотрим теперь модель, в которой источник требований обладает ограниченной мощностью и, следовательно, частота поступлений новых требований уменьшается по мере увеличения количества требований в обслуживающей системе. С помощью такого рода модели можно, например, описывать ситуации, наблюдаемые на промышленном предприятии, располагающем некоторым фиксированным количеством агрегатов определенных типов (станков, энергосиловых установок и т. п.), которые время от времени выходят из строя и требуют ремонта. Пусть М — число агрегатов, a R — число специалистов по ремонту агрегатов данного типа. Допустим, что сроки возникновения неисправностей в каждом агрегате имеют экспоненциальное распределение, т. е. поломки возникают в средне. с частотой λ, причем независимо от поведения других агрегатов.

Предположим, кроме того, что ремонт каждого неисправного агрегата требует вмешательства только одного мастера-ремонтника. Наконец, будем считать, что распределение длительностей ремонта одного неисправного агрегата определенного типа является экспоненциальным, причем средняя скорость выполнения ремонтных работ μ одинакова у всех мастеров-ремонтников и не зависит от того, какой конкретно агрегат требует ремонта.

Пусть в момент t число вышедших из строя агрегатов равняется п и, следовательно, число действующих агрегатов равняется М — п. Тогда вероятность того, что в течение очень малого интервала [t, t + h] (h > 0) произойдет поломка одного из агрегатов, которые в момент t нормально функционировали, определяется следующей приближенной:

 Скачать реферат