Модели массвого обслуживания

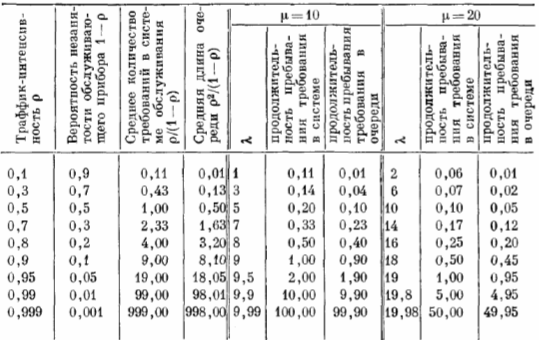
λ—количество требований, поступивших в систему за единицу времени; ρ-скорость обслуживания (количество требований, обслуживаемых за единицу времени);ρ= λ/μ- траффик-интенсивность.

Хотя все перечисленные нами показатели при достаточно больших ρ < 1 могут принимать ско

ль угодно большие значения, может пройти весьма много времени, прежде чем система достигнет равновесного состояния. При заданной скорости обслуживания μ, когда траффик-интенсивность ρ незначительна, основная доля среднего времени пребывания требования в системе связана с самой процедурой обслуживания (средняя продолжительность процедуры обслуживания равняется 1/μ); однако при возрастании ρ, т. е. при увеличении интенсивности входного потока λ, большая часть времени пребывания требования в системе (в смысле его среднего значения) обусловлена ожидание μ обслуживания в очереди. Обратимся к таблице. Пусть единицей времени является 1 ч (или 60 мин). Рассмотрим случай, когда ρ = 0,8. При этом прибор простаивает в среднем в течение 0,2 ч (т. е. каждые 12 из 60 мин), а среднее количество требований, находящихся в системе, равняется 4. При μ= 10, т. е. когда скорость обслуживания равняется 10 человек/ч (на каждое требование прибор расходует в среднем 6 мин своего рабочего времени), средняя продолжительность пребывания требования в системе равняется 0,5 ч (30 мин), а средняя продолжительность его пребывания непосредственно в очереди — 0,4 ч (или 24 мин). Если ρ = 0,8, но при этом значения как интенсивности входного потока, так и скорости обслуживания удваиваются (т. е. μ= 20), средняя продолжительность пребывания требования в системе и средняя продолжительность его ожидания начала обслуживания уменьшаются в два раза.

Случай произвольного распределения длительностей обслуживания.

Весьма несложным оказывается вычисление ожидаемого количества требований в системе массового обслуживания и средней продолжительности их пребывания в ней в том случае, когда входной поток требований характеризуется экспоненциальным распределением, а относительно вида распределения длительностей обслуживания не делается никаких специальных предположений (т. е. в случае, когда модель относится к типу M/G/1).

Пусть

Если предположить, что принята дисциплина очереди ≪первым пришел — первым обслуживаешься≫, то для средней продолжительности пребывания требования в системе обслуживания будет справедливо следующее соотношение:

Соотношения (29) и (32) часто называют формулами Поллачека — Хинчина.

Нетрудно проверить, что если плотность распределения g (f) является экспоненциальной и, следовательно, V = 1/μ2, то формулы (29), (30) и (32) преобразуются соответственно в формулы (13), (15) и (20). Эти формулы определяют также соответствующие математические ожидания в случае, когда скорость обслуживания постоянна, так как при этом V = 0. Другими словами, при

V = 0 полученные выше формулы описывают модель типа M/D/I, Обратите внимание на то, что средние значения всех указанных выше показателей являются линейными функциями V и зависят лишь от частоты поступления требований λ, траффик-интенсивности р и дисперсии

длительностей обслуживания V и не зависят ни от каких других параметров, характеризующих распределение продолжительностей интервалов между поступлениями и распределение длительностей обслуживания.

Заметим далее, что в условиях статистического равновесия

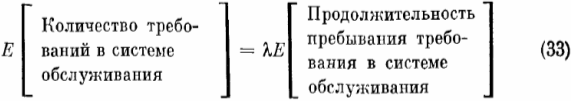
Соотношение (33), вообще говоря, имеет место и при более общих предположениях относительно режима функционирования системы массового обслуживания; в частности, оно выполняется и в случае многоканальной модели.

Дисциплина очереди при наличии приоритета.

Во многих реальных ситуациях дисциплина очереди не согласуется с правилом первым пришел — первым обслуживаешься≫. Представим себе,к примеру, молодого администратора, только что вернувшегося в свое учреждение из служебной командировки. Не исключено, что

он обнаружит на своем рабочем столе ряд телефонограмм, среди которых может оказаться и телефонограмма от какого-нибудь важного должностного лица, в подчинении которого данный молодой административный работник находится. Скорее всего, что в первую очередь он уделит внимание именно этой телефонограмме. Предположим, что требования, поступающие на вход системы обслуживания, можно подразделять на г различных категорий, каждой из которых приписывается приоритет k (k = 1, 2, . . ., г), выраженный соответствующим номером. Допустим, что приоритет падает с увеличением его номера, т. е. приоритет 1 оказывается наивысшим, а приоритет г — самым низким. Как только прибор заканчивает обслуживание того или иного требования, он немедленно переходит к обслуживанию следующего требования, отдавая при этом предпочтение тому из находящихся в очереди требований, приоритет которого оказывается наиболее высоким. (Если в очереди находится несколько требований с одинаковыми приоритетами, очередность их обслуживания определяется правилом ≪первым пришел — первым обслуживаешься≫.) В некоторых случаях, кроме того, предполагается, что при поступлении в систему обслуживания требования с более высоким приоритетом по сравнению с приоритетом требования, которое в этот момент находится в процессе обслуживания, система бросает уже начатую процедуру обслуживания и переключается на обслуживание требования с более высоким приоритетом. Другими словами, предполагается использование дисциплины нокаутирующих приоритетов. Приведенные ниже результаты относятся к случаю ненокаутирующих приоритетов. Допустим, что поток требований, обладающих приоритетом k, является пуассоновским при значении k = 1, 2, . . ., r, причем соответствующие средние частоты поступлений равняются λk.

Предположим также, что каждый приоритет k (k = 1, 2, . . ., г) характеризуется распределением длительностей обслуживания с плотностью gk (t) совершенно произвольного вида и

и будем предполагать, что о> < 1. (Это гарантирует возможность постепенного перехода системы в состояние статистического равновесия.)

Рассмотрим систему в момент времени, следующий непосредственно за завершением очередной процедуры обслуживания. Тогда для вновь поступившего требования с приоритетом k среднее время ожидания в очереди определяется формулой

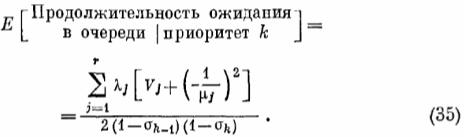
Нетрудно убедиться в том, что при r = 1 выражение (35) сводится к (32). Поскольку λk /есть вероятность того, что вновь поступившее требование обладает приоритетом k, среднее время пребывания в очереди произвольным образом выбранного требования вычисляется по следующей формуле:

 Скачать реферат