Модели массвого обслуживания

Перенесем Рп (Т) из правой части соотношения (3) в левую, разделим обе части получающегося в результате этого соотношения на h и устремим h к нулю. С помощью этих преобразований получим следующее выражение:

в момент 0). Это решение называется неустановившимся, поскольку оно непосредственно завис

ит от Т . Допустим, однако, что нами рассматриваются значения Рп (Т) при Т →∞. Если Рп(Т) стремится при этом к некоторому предельному значению (обозначим его через Рп) и если для данного предельного распределения Е [п] оказывается конечным, то говорят, что система стремится к состоянию (или достигает состояния) статистического равновесия. Назовем предельные значения Рп установившимися или стационарными вероятностями. Прилагательное «стационарный» отражает следующее свойство системы: если количество находящихся в ней требований определяется в произвольно выбранный момент t с помощью распределения Рп, то для любого h > О Рп является также вероятностью обнаружения в системе п требований в момент t + h. Значение Рп можно также интерпретировать как долю времени произвольно большого периода, в течение которой в системе находится п требований.

Если имеет место условие

то стационарные вероятности Рп всегда существуют. Величину ρ часто называют трафик интенсивностью. Решение, соответствующее равновесному состоянию Рп (Т) = Рп при любом Т, легко найти из условия dPn/dT = 0, отражающего то обстоятельство, что Рп не зависит от Т. Таким образом, для определения Рп требуется лишь приравнять нулю производные, стоящие в левых частях уравнений (4) и (5). В результате будем иметь

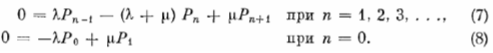
Система уравнений в конечных разностях (7) и (8) легко решается методом математической индукции. Начав с рассмотрения (8), получаем

Затем переходим к (7), рассматривая последовательно значения п = 1, 2, 3, . . .; в результате будем иметь

С учетом (6)

Обратите внимание на то, что распределение вероятностей (12) зависит только от траффик-интенсивности р = λ/μ. Поскольку ρ ( = 1 — Р0) также представляет собой ту долю полного времени с начала функционирования системы, в течение которой прибор не простаивает, то эту величину называют иногда коэффициентом использования или коэффициентом загруженности прибора. Существенным является то, что такая интерпретация сохраняет силу даже в том случае, когда не вводится никаких конкретизирующих предположений ни относительно распределения длительностей интервалов между поступлениями, ни относительно распределения длительностей обслуживания (т. е. когда модель относится к типу GI/G/1).

Если через Рп (Т | i) обозначить решение уравнений (4) и (5) при условии, что в начальный момент времени t = 0 в очереди находилось i требований, то можно показать, что

Следовательно, Рп (Т | i) стремится к Рп не медленнее, чем при изменении по экспоненциальному закону. Заметим, что при λ→μ коэффициент при Т в показателе стремится к нулю . Следовательно, интервал времени Т, в течение которого значение Рп (Т | i) станет почти равным Рп, может быть весьма продолжительным; это свойство «медленного стремления к стационарному режиму» проявляется особенно заметно при больших значениях ρ и малых значениях i.

Операционные характеристики. Математическое ожидание длины очереди можно вычислить, учитывая, что

Рассмотрим теперь интервалы времени, когда прибор не занят обслуживанием. Поскольку интервалы простоя обслуживающего прибора начинаются с моментов завершения обслуживания и заканчиваются при поступлении нового требования, продолжительности простоя приборов имеют такое же распределение, как и длительности интервалов между поступлениями требований, т. е. характеризуются распределением с математическим ожиданием 1/λ. Пусть Т настолько велико, что мы можем оперировать средними значениями операционных характеристик без каких-либо опасений . При этом продолжительность времени простоя прибора равняется ТРо = Т (1 — ), а число отдельных периодов времени, в течение которых прибор оказывается в пределах Т незанятым, равняется Т (1 — ρ)/( 1/λ) = λТ (1 — ρ). Поскольку периоды обслуживания и периоды простоя являются строго чередующимися, то λТ (1 — ρ). определяет также число занятых периодов в течение полного периода Т, а ρТ есть суммарная продолжительность периодов, когда прибор занят обслуживанием. Следовательно,

Формулы (16) и (17), вообще говоря, справедливы при любом распределении длительностей обслуживания (т. е. применимы и в случае модели M/G/1)

Рассмотрим теперь плотность распределения для продолжительности пребывания требования в системе обслуживания. Время, в течение которого требование находится в системе, складывается из продолжительности ожидания им обслуживания в очереди и длительности самой процедуры обслуживания. Теперь предположим, что система находится в состоянии статистического равновесия, так что каждое из вновь поступающих требований с вероятностью Рп, определяемой формулой (12), обнаруживает впереди себя п уже ожидающих обслуживания требований. Допустим, что для очереди принята дисциплина «первым пришел — первым обслуживаешься». Тогда полное время пребывания требования в системе представляет собой сумму п +1 независимых выборок из множества значений, принимаемых случайной переменной, которая характеризуется экспоненциальным распределением, т. е. описывается гамма-распределением с плотностью:

При фиксированном значении р средняя продолжительность пребывания требования в системе, так же как и средняя продолжительность его пребывания в очереди, обратно пропорциональна скорости обслуживания μ.

Анализ на чувствительность. Основные операционные характеристики одноканальной системы массового обслуживания с дисциплиной очереди «первым пришел — первым обслуживаешься» приведены в таблице на рис. 20.3 как функции ρ и μ. Обратите внимание на то, что при возрастании траффик-интенсивности р ожидаемые значения таких параметров, как число находящихся в системе требований, длина очереди, полное время пребывания требования в системе и чистое время его пребывания в очереди, также начинают быстро возрастать.

 Скачать реферат