Модели массвого обслуживания

Можно доказать, что если рассматривать систему в произвольный момент времени t, то

Следовательно, если дисперсия в формуле (13) отлична от нуля, то средняя продолжительность ожидания с момента t до появления первого такси, превышает (1/2) -(1/λ). Заметим, что в случае экспоненциального расп

ределения длительностей интервалов между последовательными появлениями дисперсия равняется 1/λ2 и, следовательно, среднее время ожидания с момента t до появления такси равняется 1/λ. Если же дисперсия принимает значения, превышающие 1/λ2,то среднее время ожидания свободного такси (отсчитываемое от момента t) оказывается на самом деле большим, чем среднее значение длительности интервала между появлениями свободных такси. Этот результат может показаться на первый взгляд несколько удивительным.

Распределение Эрланга. Другим важным частным случаем распределения длительностей интервалов между последовательными поступлениями требований на обслуживание является распределение Эрланга

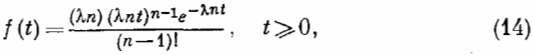
где п — положительное целое число. Для математического ожидания и дисперсии соответственно имеем

Е [t] = 1/λ, Var [t] = 1/n λ2 (15)

(Это распределение часто обозначают символом Еп.)

Произведя в (14) замену пλ -> λ, мы получим гамма-распределение (8).

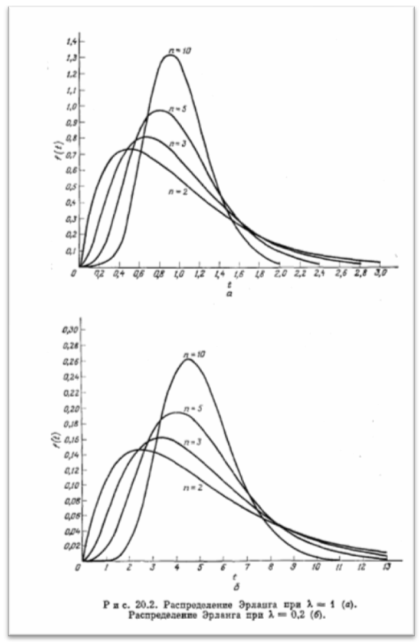
Варьируя надлежащим образом значениями К и п, мы можем использовать распределение Эрланга в качестве хорошего приближения распределений других видов; ряд графиков, иллюстрирующих поведение f(t) при некоторых частных значениях λ и п, приведен на рисунке. Следует обратить внимание на то, что при п = 1 распределение Эрланга становится тождественным экспоненциальному распределению. Отметим также, что при п → ∞, когда

Var [t] →0, распределение Эрланга соответствует случаю регулярного (или строго периодического) поступления, т. е. случаю, когда длительности (1/λ) интервалов между поступлениями одинаковы и не меняются со временем (т. е. являются константами)

3 Распределение вероятностей для длительностей обслуживания

Рассуждения, связанные с конкретизацией плотности вероятности для длительностей обслуживания, в значительной степени схожи с рассуждениями, позволяющими установить форму распределения длительностей интервалов между поступлениями требований во входной контур системы. Мы исходим из предположения, что каждый прибор обслуживания (или канал) может в одно и то же время обслуживать только одно требование.

Допустим, что для каждого рассматриваемого прибора длительности следующих один за другим интервалов обслуживания распределены независимым и идентичным образом и могут быть описаны с помощью плотности распределения, представляющей собой непрерывную функцию. Пусть

Так, например, если за единицу измерения времени принимается 1 ч и если μ = 5, т. е. в течение 1 ч действующий обслуживающий прибор успевает обслужить пять требований, то среднее время обслуживания одного требования составляет 1/μ = 0,2 ч. Аналогично, если на обслуживание одного требования в среднем уходит 30 мин, то скорость обслуживания составляет μ = 2 требования в час (при этом в расчет принимается только то время, когда прибор занят обслуживанием). Часто предполагают, что распределение длительностей обслуживания является экспоненциальным:

Основной мотив, побудивший нас принять такое предположение, остается прежним — он заключается в стремлении упростить математическую сторону вопроса. Однако предположение о том, что механизм обслуживания функционирует в режиме экспоненциального распределения, может одновременно служить некоторым ориентиром при анализе операционных характеристик любой системы массового обслуживания, поскольку в нем находят отражение особенности систем «экстремального» типа, т. е. систем, в которых обслуживающие приборы не обладают памятью. В случае показательного распределения длительностей обслуживания вероятность завершения обслуживания клиента в любой последующий интервал времени (t, t+h) не зависит от того, сколько времени уже потрачено на обслуживание этого требования. Таким образом, если в момент t требование уже обслуживалось и мы рассматриваем систему в момент (t+h), то в силу (4)

Модель самообслуживания. Предположим теперь, что в отличие от рассмотренного выше случая (когда система содержала единственный обслуживающий прибор) в момент 0 каждый из М клиентов приступает к самообслуживанию. Допустим, что длительности самообслуживания у каждого из клиентов распределены по уже известному нам экспоненциальному закону (4). Такое предположение в условиях самообслуживания представляется вполне логичным.

Рассмотрим очень малый интервал времени (Т, T+h), где h > 0. Тогда, поскольку каждый клиент действует в процессе самообслуживания независимым образом, с помощью приближенной формулы (6) получаем

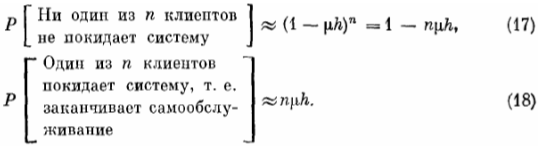
При этом, учитывая, что h -> 0, мы в процессе обоснования (18) можем ограничиться рассмотрением лишь таких событий, когда на интервале (Т, Т + h) либо ни один из п клиентов не успеваем закончить процедуру самообслуживания, либо заканчивает самообслуживание один из них, т. е. мы пренебрегаем вероятностями того,что в данном интервале самообслуживание заканчивают два или большее число клиентов, считая эти вероятности величинами болем высокого порядка малости.

Другими словами, если в момент T+h в системе находится п клиентов, то предполагается, что можно учитывать лишь а) вероятность того, что в момент Т в ней также было п клиентов и не наблюдалось ни одного случая их выхода из системы, и б) вероятность того, что в момент Т число клиентов внутри системы равнялось п + 1 и наблюдался случай выхода одного клиента из данной системы (при этом должно выполняться условие М > п), т. е.

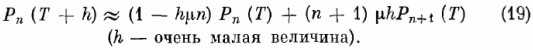
Перенесем Рп (Т) в левую часть (19), разделим обе части получаемого в результате соотношения на h и устремим h к нулю; после этого будем иметь

Терминология и обозначения. Знакомясь с литературой по теории массового обслуживания, нетрудно заметить, что употребляемая в этой области терминология в определенной степени стандартизирована, а обозначения (которые часто называют обозначениями Кендалла) унифицированы. При этом для обозначения той или иной модели используют три символа: первый характеризует входной поток требований, второй — распределение длительностей обслуживания и третий — число приборов в обслуживающей системе. Приведем перечень общепринятых символов, характеризующих распределения вероятностей, которые ставятся в соответствие моделям массового обслуживания:

 Скачать реферат