Модели массвого обслуживания
P [Отсутствие поступлений в любом интервале, имеющем длину
h]=![]() = 1
= 1 ![]() +
+ ![]() +
+![]() +… . (5)
+… . (5)
Для достаточно малых положительных значений h член 1 P [Отсутствие поступлений в любом интервале, имеющем длину h] ≈1 Весьма наглядный, хотя и не совсем корректный, способ обоснования правомерности очередного математического хода заключается в принятии следующего допущения: на интервале достаточно малой продолжительности h количество поступлений не превышает единицы [т. е. количество поступлений внутри достаточно малого интервала (Т, T+h) равняется либо нулю, либо единице]. Поскольку приближенная формула для вероятности отсутствия поступлений на интервале
(Т, T+h) имеет вид (6), мы приходим к следующему выражению:
P [Отсутствие поступлений в любом интервале, имеющем длину h] ≈ Более последовательный метод вывода формулы (7) связан с разложением в ряд Тейлора точного выражения для вероятности единичного поступления в интервале (Т, Т+h); после этого потребовалось бы показать, что для достаточно малых значений h в упомянутом разложении можно пренебречь всеми членами, исключая Допустим, например, что λ равняется четырем поступлениям в час. Тогда вероятность отсутствия поступлений на интервале 0,1 ч, согласно (5), равняется 0,96079, а согласно приближенной формуле (6), 1 — 0,04 = 0,96; вероятность одного поступления
на указанном интервале, согласно (7), равняется 0,04. Если плотность распределения длительностей интервалов между поступлениями требований на обслуживание имеет экспоненциальный вид (2), то плотность распределения полного времени у для произвольным образом выбранного ряда из п последовательных поступлений определяется следующей формулой:
g(y)= где п — положительное целое число. Величину у можно интерпретировать как сумму п независимых выборок из экспоненциального распределения (2). Тогда
P[Полное время для любой последовательности из n поступлений равно или меньше Т]= 1- в чем легко убедиться, прибегнув к многократному интегрированию по частям.
Наконец, следует отметить, что предположение об экспоненциальном характере распределения длительностей интервалов между поступлениями равносильно следующему утверждению: распределение вероятностей попадания п поступлений в произвольным образом выбранный интервал продолжительностью Т является пуассоневским, т. е.
Теперь нам ясно, почему термины «экспоненциальный закон распределения поступлений» и «пуассоновский процесс» являются синонимами. (Иногда используется термин «марковский процесс» или, в сокращенной записи, «М-процесс»)
Легко убедиться, что из (9) и (10) вытекает следующее равенство:
Приведенные выше формулы находят непосредственное применение для описания процессов чистого рождения.
Рассмотрим систему, в которой в начальный момент 0 требования отсутствуют. Предположим, что процесс поступления (рождения) является пуассоновским, и допустимым, что поступившие в систему требования на выходе не появляются (т. е. остаются в системе в течение бесконечно большого интервала времени).
Попытаемся теперь дать краткое (но более строгое) обоснование того, что из некоторого вполне определенного ряда предположений относительно свойств процесса поступления вытекает показательное распределение длительностей интервалов между поступлениями, и входной поток, таким образом, является пуассоновским.
Мы исходим из следующих постулатов:
(A) Длительности интервалов между последовательными поступлениями взаимонезависимы и распределены идентичным образом; при этом вероятность поступления требования в интервале (Т, Т + К) зависит лишь от h и не зависит от Т. Плотность вероятности, соответствующую такому характеру входного потока, обозначим через f(t).
(Б) Существует некоторая ненулевая вероятность поступления в течение любого интервала h > 0.
(B) При достаточно малых значениях h количество поступающих заявок не превышает единицы.
Предположим для простоты, что система начинает функционировать, начиная с момента 0, причем первое поступление имеет место в момент t (t≥0). Отсюда следует, что f(t) представляет собой плотность вероятности как для продолжительности интервалов между двумя поступлениями, так и для фактического времени появления первого требования.
Определим
Пусть t = x есть время первого поступления, причем, согласно постулату (В), в момент х поступает единственное требование. Учитывая постулат (А), мы можем написать Легко убедиться в том, что функция Рп (Т), определяемая формулой (XI), действительно удовлетворяет уравнению (X); для этого достаточно продифференцировать выражение (XI) по Т. Таким образом, формула (X) нами доказана.
Случай с такси. Приведем пример, иллюстрирующий свойство экспоненциального распределения «не помнить о прошлом» и одновременно демонстрирующий в некотором смысле парадоксальную ситуацию, которая может иметь место в системах массового обслуживания. Представим себе, что мы пытаемся поймать такси в каком-нибудь месте на одной из центральных площадей города. Допустим, что мимо этого места каждые 30 с проходит в среднем одно свободное такси, т. е. средняя продолжительность интервала между появлениями такси в заданной точке равняется 1/λ = 30 с.
Предположим, что мы пытаемся поймать такси, начиная с некоторого произвольным образом выбранного момента времени. Сколько в среднем секунд нам придется ждать появления свободного такси? Многие отвечают, что ждать придется 15 с. Так ли это? Ниже будет показано, что такой ответ был бы правильным лишь при условии, что свободные такси появляются у места, где мы их ловим, строго через каждые 30 с. Если имеет место хотя бы некоторый разброс интервалов между появлениями свободных такси у выбранного нами места, продолжительность нашего ожидания всегда будет больше 15 с.
![]() (6)
(6)
![]() (для достаточно малых значений h) (7)
(для достаточно малых значений h) (7)
![]() (как бесконечно малыми более высокого порядка). В контексте символ ≈ всюду означает, что в разложении функции в ряд мы пренебрегаем членами «более высокого порядка малости».
(как бесконечно малыми более высокого порядка). В контексте символ ≈ всюду означает, что в разложении функции в ряд мы пренебрегаем членами «более высокого порядка малости».
![]() y≥0 (гамма-распределение) (8)
y≥0 (гамма-распределение) (8)
![]() =
=
![]() , (9)
, (9)
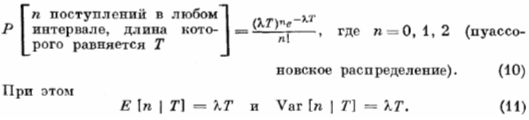
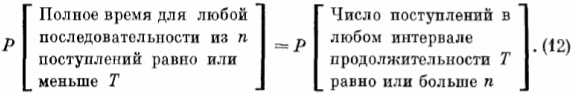


Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
