Доказательство утверждения, частным случаем которого является великая теорема Ферма

Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.

********

Случай 11

(16)

(17)

height=21 src="images/referats/7515/image235.png">(18)

(19´)

Из (16) и (17) имеем:

Учитывая (14) и (19´), можно получить разность другим способом:

- => .

Следовательно, =-=> 2t = - 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) cи b – четные, чего не должно быть.

Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.

Случай 12

(16´)

(17´)

(18´)

(19),

т.е. по сравнению с предыдущим случаем 11 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 11.

Действительно, из (16´) и (17´) имеем:

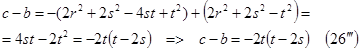
Учитывая (14) и (19), можно получить разность другим способом:

=> .

Следовательно, -==> 2t = - 4r (≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) cи b – четные, чего не должно быть.

Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.

*******

Случай 13

(16)

(17)

(18´)

(19´)

Из (16) и (17) имеем:

Учитывая (14) и (19´), можно получить разность другим способом:

- => .

Следовательно, =-=> 2t = - 4r (≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) cи b – четные, чего не должно быть.

Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.

********

Случай 14

(16´)

(17´)

(18)

(19),

т.е. по сравнению с предыдущим случаем 13 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 13.

Действительно, из (16´) и (17´) имеем:

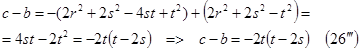
Учитывая (14) и (19), можно получить разность другим способом:

=> .

Следовательно, -==> 2t = - 4r (≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) cи b – четные, чего не должно быть.

Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.

***********

Вывод.

1. Таким образом, случаи 9,…, 14 новых возможных решений уравнения (15) не выявили.

2. Условие 1 (продолжение) нами полностью рассмотрено.

**********

Условие 2 (продолжение).

Ранее мы отмечали, что уравнение (15) симметрично для с и b, поэтому с и bмогут меняться своими выражениями (Cи В). Это свойство нами было названо «новым свойством ».

 Скачать реферат