Применение теории массового обслуживания в исследовании рынка

3. СМО с типом дисциплины выбора требований случайным способом;

4. СМО с типом дисциплины выбора требований в соответствии с присвоенными приоритетами.

Другими вариантами классификаций могут быть следующие.

Поступление требований может быть единичным и групповым.

Требования могут обслуживаться параллельно работающими приборами, но может быть и система, в которой приборы располож

ены последовательно так, что как только будет обслужено требование первым прибором, то начнет обслуживаться и другое и т.д.

Интенсивность обслуживания прибором может быть постоянной или зависеть от длины очереди, приоритетов или каких-либо других факторов.

Наконец, системы массового обслуживания различают по характеру входного потока и по характеру обслуживающих устройств.

По характеру входной поток требований разделяется на детерминированный поток требований и стохастический (рис. 2).

Детерминированный входной поток может быть двух видов. В первом случае требования поступают через равные промежутки времени. Другим видом детерминированного потока является поток, в котором требования поступают по известной программе – расписанию, когда моменты поступления новых требований известны заранее.

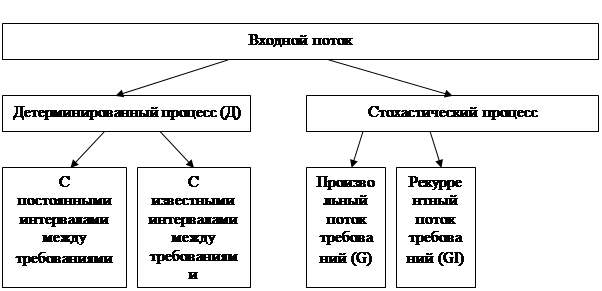
Рис. 2. Классификация входного потока

Если промежутки времени между поступлениями требований случайны, то это будет стохастический процесс.

Стохастический поток требований подразделяется на три вида: поток с произвольными стохастическими свойствами, рекуррентный поток и совершенно случайный или пуассоновский поток требований.

Произвольный поток требований характеризуется тем, что на него не накладывается никаких ограничений на стохастическую независимость интервалов между поступлениями требований, а также на характер вероятностных законов, описывающих интервалы между требованиями.

Входной поток называется рекуррентным, если он характеризуется следующими свойствами:

a) продолжительность интервалов между поступлениями требований стохастически независимы;

b) продолжительность интервалов описывается одной и той же плотностью распределения.

Входной поток называется совершенно случайным или простейшим, если для него характерно:

a) продолжительность интервалов между поступлениями требований статистически независимы;

b) продолжительность интервалов описывается одной и той же плотностью распределения;

c) вероятность поступления требований на достаточно малом интервале Δt зависит только лишь от величины Δt (это свойство называется стационарностью или однородностью прихода);

d) вероятность поступления требований на интервале Δt не зависит от предыстории процесса;

e) характер потока требований таков, что в любой момент времени может поступить только одно требование.

Таким образом, простейший поток требований или совершенно случайный поток – это поток, определяющейся свойствами стационарности, ординарности и отсутствием последствия одновременно.

Предположения о совершенно случайном входном потоке требований эквивалентно тому, что плотность распределения интервалов времени между последовательными поступлениями требований описывается экспоненциальным законом:

(1.1)

где λ– интенсивность поступления заявок в систему.

Если интервалы распределены по экспоненциальному закону, то процесс пуассоновский. Такие процессы называются М-процессами (Марковскими).

Кроме закона Пуассона часто применяется закон распределения Эрланга.

(1.2)

Обозначения Кендалла систем массового обслуживания.

Аналогично входному потоку процесс обслуживания требований может быть детерминированным и стохастическим.

Детерминированный процесс обслуживания характеризуется постоянной величиной времени обслуживания

где – интенсивность обслуживания, которая представляет собой число требований, обслуживаемых в единицу времени.

Стохастический процесс обслуживания может быть произвольным, рекуррентным или совершенно случайным, как и при описании входного потока требований [15].

При рассмотрении систем массового обслуживания часто используются обозначения предложенные Кендаллом. Они позволяют описать СМО с помощью следующих трех элементов: вид входного потока, распределение продолжительности обслуживания, число обслуживающих приборов.

Используются следующие обозначения:

M – пуассоновское или экспоненциальное распределение;

D – постоянная величина;

Ek – распределение Эрланга;

G – общий вид распределения;

GI – рекуррентный входной поток.

Общий вид, характеризующий систему массового обслуживания, представляет собой следующую последовательность:

где Н1 – характеристика входного потока, H2 – характеристика времени обслуживания прибора, i – число приборов.

Например, система M /D /s – система с s приборами, обслуживающая поступающие требования за строго определенный интервал времени, поступающие требования образуют пуассоновский поток [16].

Классификация систем массового обслуживания по характеру обслуживания.

СМО с отказами.

Одноканальная СМО содержит один канал (n = 1), и на ее вход поступает пуассоновский поток заявок Пвх интенсивность (среднее число событий в единицу времени) которого inПвх=λ. Так как интенсивность входящего потока может изменяться во времени, то вместо λ записывают λ(t). Тогда время обслуживания каналом одной заявки Тоб распределено по показательному закону и записывается в виде: , где λ – интенсивность отказов.

Состояние СМО характеризуется простаиванием или занятостью ее канала, т.е. двумя состояниями: S0 – канал свободен и простаивает, S1 – канал занят. Переход системы из состояния S0 в состояние S1 осуществляется под воздействием входящего потока заявок Пвх, а из состояния S1 в состояние S0 систему переводит поток обслуживании Поб: если в данный момент времени система находится в некотором состоянии, то с наступлением первого после данного момента времени СМО переходит в другое состояние. Плотности вероятностей перехода из состояния S0 в S1 и обратно равны соответственно λ и µ. Граф состояний подобной СМО с двумя возможными состояниями приведен на рис. 3.

Рис. 3. Граф состояний одноканальной СМО с отказами

Для многоканальной СМО с отказами (n > 1) при тех же условиях состояния системы обозначим по числу занятых каналов (по числу заявок, находящихся в системе под обслуживанием, так как каждый канал в СМО либо свободен, либо обслуживает только одну заявку). Таким образом, подобная СМО может находиться в одном из следующих (n+1) состояний: s0 – все n каналов свободны; s1 – занят только один из каналов, остальные (n-1) каналов свободны; si – заняты i – каналов, (n-i) каналов свободны; sn – заняты все n каналов. Граф состояний такой СМО приведен на рис. 4.

 Скачать реферат