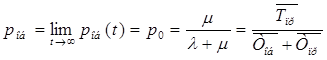Применение теории массового обслуживания в исследовании рынка

Рис. 4. Граф состояний многоканальной СМО с отказами

При этом имеет место а

Пользуясь общим правилом составления дифференциальных уравнений Колмогорова, можно для приведенных на рис. 2 и

рис. 3 графов состояний составить системы дифференциальных уравнений:

a) например, для одноканальной СМО (рис. 2) имеем:

b) для многоканальной СМО (рис. 3) соответственно имеем:

……………………………

……………………………

Решив первую систему уравнений, можно найти значения p0(t) и p1(t) для одноканальной СМО и построить графики при трех случаях: 1) λ >µ; 2) λ=µ; 3) λ<µ (рис. 5 а, б, в). Можно также определить предельную пропускную способность СМО. Решение второй системы уравнений для многоканальной СМО в аналитическом виде получить вручную сложно, и его обычно получают с помощью ЭВМ в численном виде.

Рис. 5 а, б, в, г

В целом, характеристики одноканальной СМО с отказами приведены ниже и особых пояснений не требуют [17].

Таблица 1. Характеристики одноканальной СМО с отказами

СМО с ожиданием.

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание – простейший поток с интенсивностью λ. Интенсивность потока обслуживания равна µ (т.е. в среднем непрерывно занятый канал будет выдавать µ обслуженных заявок). Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), т.е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость. Граф состояний СМО в этом случае имеет вид, показанный на рис. 6.

Рис. 6. Граф состояний одноканальной СМО с ожиданием

 Скачать реферат