Применение теории массового обслуживания в исследовании рынка

Состояния СМО имеют следующую интерпретацию:

S0 – канал свободен;

S1 – канал занят (очереди нет);

S2 – канал занят (одна заявка стоит в очереди);

……………………………………………………

Sn – канал занят (n-1 заявок стоит в очереди);

………………………………………………….

SN – канал занят (N-1 заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраи

ческих уравнений:

(1.11)

где ρ=λ/µ; n – номер состояния.

Решение приведенной выше системы уравнений (1.10) для нашей модели СМО имеет вид:

(1.12)

(1.13)

Тогда

Следует отметить, что выполнение условия стационарности для данной СМО необязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать N-1), а не соотношением между интенсивностями входного потока, т.е. не отношением λ/µ=ρ.

Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной (N-1):

1. вероятность отказа в обслуживании заявки:

(1.14)

2. относительная пропускная способность системы:

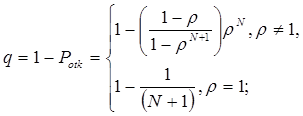(1.15)

3. абсолютная пропускная способность:

(1.16)

4. среднее число находящихся в системе заявок:

(1.17)

5. среднее время пребывания заявки в системе:

(1.18)

6. средняя продолжительность пребывания клиента (заявки) в очереди:

(1.19)

7. среднее число заявок (клиентов) в очереди (длина очереди):

. (1.20) [2, 89 – 92].

Теперь рассмотрим более подробно СМО, имеющую n-каналов с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживаний – интенсивность µ. Необходимо найти предельные вероятности состояний СМО и показатели ей эффективности.

Система может находиться в одном состоянии S0, S1, S2,…, Sk,…, Sn,…, нумеруемых по числу заявок, находящихся в СМО: S0 – в системе нет заявок (все каналы свободны); S1 – занят один канал, остальные свободны; S2 – заняты два канала, остальные свободны;…, Sk – занято k каналов, остальные свободны;…, Sn – заняты все n каналов (очереди нет); Sn+1 – заняты все n каналов, в очереди одна заявка;…, Sn+r – заняты все n каналов, r заявок стоит в очереди, …. Граф состояний показан на рисунке 7.

Рис. 7. Граф состояний многоканальной СМО с ожиданием

Обратим внимание, что по мере увеличения в СМО от 0 до n увеличивается число каналов обслуживания. При числе заявок в СМО, большем, чем n, интенсивность потока обслуживания сохраняется равной nµ.

Формулы для предельных состояний СМО с ожиданием выглядят следующим образом:

(1.27)

(1.28)

(1.29)

Вероятность того, что заявка окажется в очереди равна:

(1.30)

Для n-канальной СМО с ожиданием, используя прежние формулы, можно найти:

· среднее число занятых каналов:

(1.31)

· среднее число заявок в очереди:

(1.32)

· среднее число заявок в системе:

(1.31) [4, 349 – 360].

1.2 Имитационное моделирование систем массового обслуживания

1.2.1 «Когда другие методы беспомощны…»

Несмотря на то, что математическое программирование и стохастическое моделирование имеют широкий диапазон применения, при рассмотрении многих важных задач организационного управления возникает необходимость обращаться к совершенно иным методам анализа.

Методы математического моделирования пока не смогут обеспечить исчерпывающего анализа таких задач организационного управления, как:

1. Формирование инвестиционной политики при перспективном планировании. Инвестиционная политика крупных фирма должна, в частности, учитывать финансовое обеспечение научно-исследовательских и опытно-конструкторских работ при создании новых видов продукции, возможности расширения рынка сбыта, критериальные оценки основных проектов, оценку степени риска при планировании тех или иных комплексов работ, источники финансирования (кредит, привлечение капитала продажей акций и т.д.), увеличение фонда заработной платы, размещение и сокращение финансовых активов, сравнительную оценку вариантов слияния с другой фирмой и приобретения последней и т.п. Полноценная операционная модель, с помощью которой можно было бы анализировать различные варианты инвестиционной политики, должна учитывать стохастическую природу и динамический характер инвестирования, а также предусматривать способ просеивания огромного количества стоящих перед фирмой альтернатив.

2. Выбор средств обслуживания (или оборудования) при текущем планировании. При этом рассматривались задачи определения количества контрольных прилавков в большом торговом центре, количества бензоколонок на бензозаправочной станции и количества лифтов в строящемся здании. Можно привести много других примеров, в которых рассматриваются вопросы распределения кадров, планировка заводских помещений, выбор мощности оборудования и т.д. Типичными вопросами, возникающими в связи с решением задачи выбора средств обслуживания или оборудования, являются вопросы, начинающиеся словами: сколько?, каких размеров? и как разместить?.

3. Разработка планов с обратной информационной связью и операционных предписаний. Примеры такого рода задач также многочисленны, хотя они не сразу могут прийти на ум тем, кто не имеет достаточного профессионального опыта. К важным задачам данного класса относится, например, задача выработки правил составления календарных планов на предприятиях с мелкосерийным производством, комбинатах по ремонту различных изделий, вычислительных центрах и т.д. Эти предписания, или операционные алгоритмы, должны учитывать гарантийные сроки выполнения заказов, потребности в обслуживании, наличные ресурсы, производственные мощности, темпы повышения квалификации рабочих (или приток дополнительной квалифицированной рабочей силы), уровень снабжения сырьем. По мере поступления информации о новых уже выполненных заказах предприятие сталкивается с задачей уточнения или полного пересмотра своих планов-графиков.

 Скачать реферат