Методы исследования операций

Дальнейшее увеличение параметра не приводит к росту прибыли, поэтому ограничиваемся значением параметра Д=16000.

5. Оптимизация распределения ресурса с помощью табличного алгоритма динамического программирования.

Имеем задачу оптимального распределения фиксированного количества ресурса по вариантам производства, различающимся во времени, в пространстве и по технологиям (тип I).

Общая постановка задачи.

Имеется количество некоторого ресурса, который можно использовать в вариантах производства. Известны функции эффекта, получаемого в каждом варианте при использовании ресурса в количестве . Необходимо так распределить по вариантам, чтобы суммарный эффект был максимальным.

Модель.

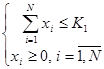
Алгоритм решения задачи динамического программирования для двухшагового процесса с использованием рекуррентных соотношений Беллмана.

Пусть известны два варианта распределения выделенных средств и соответствующие им функции эффекта от использования средств в объеме . Задан объем денежного ресурса . Его следует распределить между двумя вариантами так, чтобы суммарный эффект от вложения средств был максимальным. Поскольку имеется два варианта распределения средств, то процесс является двухшаговым. Запишем рекуррентные соотношения Беллмана для двухшагового процесса:

Обозначим максимальный эффект от распределения денежных средств через

,

где - оптимальное распределение средств -ому варианту при начальном их объеме .

Шаг 1. Пусть имеется одношаговый процесс для одного второго шага, то есть при остатке ресурса . Тогда максимальный эффект за один второй шаг запишется в виде:

.

Здесь – неизвестно, так как не знаем распределение первого шага. Тогда запишем оптимальный объем средств, выделенных второму варианту, - как функцию :

.

Получили записанный в общем виде аргумент, приносящий максимальный эффект третьему варианту. Тогда максимальный эффект на первом шаге с учетом введенных обозначений запишется в виде:

.

Шаг 2. Имея решение первого шага, решим двухшаговую задачу. Запишем максимальный эффект за первый и второй шаг:

Постановка задачи. Имеется первоначальное количество денежного ресурса, в размере 100000 ден. ед. Его необходимо распределить между двумя отделами фирмы – рекламным и технологическим, так, чтобы суммарный эффект был максимальным. Известны функции эффекта, представленные в таблице:

 Скачать реферат