Возможности использования непроизвольной памяти младших школьников при формировании табличных случаев сложения и вычитания однозначных чисел

Разгадай закономерности, вставь в "окошко" число.

Полезно сделать схематические весы с подвижными стрелками ( вверх и вниз), заготовить модели гирь и различных предметов и предлагать детям с этим наглядным пособием различные задания на сос

тав чисел в пределах 20.

На современном этапе развития школьного образования учитель получил возможность выбирать учебники, по которым он может обучать детей. Поэтому ряд школ в нашей стране работают по программе и учебнику Н.Б.Истоминой. Такой выбор сделан не случайно. В этом учебнике нашли отражение не только современные методы и средства обучения, организационные формы учебной деятельности учащихся, но и система продуктивных заданий, с которыми интересно работать как детям, так и учителю.

Система заданий, представленных в учебнике математики Н.Б.Истоминой, способствует реализации взаимосвязи развития мышления младших школьников и усвоения ими знаний, умений и навыков. Кроме того, эти задания обеспечивают осознанное овладение обобщенным способом действия, предусматривают вариативность упражнений, как по содержанию, так и по форме подачи, а также своевременную установку на запоминание табличных случаев арифметических действий.

Рассмотрим это на примере конкретного урока по теме "Сложение однозначных чисел с переходом в другой разряд и соответствующие случаи вычитания".

1. На доске записаны два столбика выражений:

6+6 6+4+2

5+8 5+5+3

8+6 8+2+4

7+8 7+3+5

Предлагается сравнить выражения первого и второго столбиков и объяснить, чем они похожи и чем отличаются.

Выясняется, что выражения каждого столбика есть сумма чисел, первые слагаемые у них одинаковые. Этим они похожи. Отличаются тем, что в первом столбике записана сумма двух слагаемых, а во втором – трех.

Учитель предлагает вычислить значения суммы первого столбика. Дети называют числа: 12, 13, 14, 15.

Проводится беседа:

Давайте вспомним, как складываются такие числа. (Первое слагаемое дополняем до 10. для этого к 6 прибавим 4, получаем 10, к 10т прибавляем 2, получаем 12).

Аналогично учащиеся объясняют способ действия для других случаев этого столбика.

Какую роль играет второй столбик в этом задании? (Выражения второго столбика выполняют роль помощника. Они помогают быстро найти значения сумм первого столбика.)

Далее предлагается сравнить значения сумм с числами, записанными в таблице, и прочитать полученное слово:

Представьте, что мы попали на цирковое представление, вы его участники. На цирковой арене понадобится ваши знания таблиц сложения и вычитания в пределах 20.

2. На арене клоун со своим песиком Фунтиком, который выложил ряды чисел:

1 2 3 4 5 6 7 8 9 10 11

1 2 3 4 5 6 7 8 9 10 11 12

Клоун пояснил, что это "волшебные" ряды, в первом ряду надо подобрать два таких числа, которые в сумме дадут число 12, а во втором ряду – число 13.

Дети называют суммы, учитель записывает их на доске:

1+11, 2+10, 3+9, 4+8, 5+7, 1+12, 2+11, 3+10, 4+9, 5+8, 6+7.

Какое число в первом ряду не было названо? (6)

С каким числом его надо сложить, чтобы получить число 12? (6+6=12)

Какую закономерность вы заметили?

Запишите по этому же правилу такие ряды чисел, чтобы составить суммы, значения которых равны: 14, 15, 16.

Задание выполняется по рядам. При проверке учащиеся по цепочке называют соответствующие суммы чисел.

На доске выставлены карточки с числами:

Клоун вместе с Фунтиком предлагает задание: "Разгадай правило, по которому числа, записанные в карточках, связаны между собой, и заполни пустые окошки".

Ученики поясняют, что на карточках два числа в сумме дают третье число и называют пропущенные числа (9, 8, 6, 7, 9, 11)

Клоун меняет задание и предлагает расставить знаки арифметических действий так, чтобы равенства были верные:

8 * 7 * 6 = 9 15 * 7 *1 = 9

4 * 8 * 3 = 9

Учащиеся так объясняют постановку знаков: в первом равенстве три однозначных числа, если поставим знаки "+" и "-", тогда 8 "плюс" 7, получим 15, 15 "минус" 6, будет 9, равенство верное и т.д.

Выясняется, чем похожи эти три равенства. Какое равенство является лишним?

Учащиеся поясняют: во всех трех равенствах значения выражений равно 9, в каждом равенстве слева по три числа. Этим равенства похожи. А, отвечая на второй вопрос, одни учащиеся назвали лишним третье равенство, так как оно содержит двузначное число 15; другие, ориентируясь на знаки арифметических действий, назвали вопрос, потому что в первом и третьем равенствах знаки идут в таком порядке: "+" и "-", а во втором сначала идет знак "-", а потом знак "+".

5. На арене жонглеры. Выясняется, какими предметами они

жонглируют. Проводится беседа:

По какому признаку можно разбить все предметы на две группы? (По цвету, размеру и форме).

Какому разбиению соответствуют выражения, записанные в столбиках:

8+3 6+5 7+4

11-8 11-6 11-7

11-3 11-5 11-4

(В первом столбике предметы разбиты по форме – 8 обручей и 3 булавы; во втором по размеру - 5 больших предметов и 6 маленьких; в третьем по цвету –7 красных и 4 синих предмета).

Найдите значения выражений и объясните, как вычислить значение разности, используя сумму. (Учащиеся вспоминают правило взаимосвязи между сложением и вычитанием и объясняют: значения суммы 8 и 3 равно 11; если из суммы 11 вычесть первое слагаемое 8, то получится второе слагаемое 3 и наоборот).

Аналогично учащиеся находят значения выражений второго и третьего столбиков.

6. "Математические" фокусы:

а) Задумайте любое число меньше 10, прибавьте к нему число 6, назовите число, которое получилось, а я скажу, какое число было задумано.

б) Задумайте любое однозначное число, прибавьте к нему число 7, а теперь из полученного значения суммы надо вычесть задуманное число. У вас в ответе получилось 7. Кто понял, как это узнать?

7. На арену выходит Дарья с дрессированными голубями. Ей надо 15 голубей рассадить на два обруча.

Догадайтесь, как она могла это сделать, составьте соответствующие равенства и запишите их:

14+1=15 13+2=15 12+3=15

11+4=15 10+5=15 8+7=15

8. Запишите равенства, которые отмечены на числовых лучах. Запишите их.

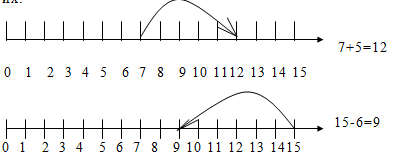
9. Можно ли утверждать, что значения выражений во всех столбиках одинаковые?

(Проблемные ситуации заданий направляют исследовательскую деятельность учащихся).