Логический анализ суждений как необходимый компонент познавательных учебных действий

Любом, только один.

Через точку, не лежащую на данной прямой, проходит прямая, параллельная данной.

Только одна;

Не единственная;

Любая.

два угла треугольника равны, треугольник равнобедренный.

Когда, такой;

Если, то;

Некоторые, если.

катеты одного прямоугольного треугольника соответственно равны катетам другого, такие треугольники равны.

Когда, такой >Некоторые, если

Если, то;

точки из двух параллельных прямых равноудалены от другой прямой.

Некоторые, каждой;

Все, некоторой;

Все, каждой.

У треугольника хотя бы два угла острые.

Некоторого;

Любого;

Равного.

в четырехугольнике две стороны равны и параллельны, этот четырехугольник – параллелограмм.

Когда, если;

Если, то;

Тогда и только тогда, когда.

многоугольник составлен из нескольких многоугольников, его площадь равна сумме площадей этих многоугольников.

Если, то;

Тогда и только тогда, когда;

Когда, если.

В треугольник можно вписать окружность.

Любой;

Некоторый;

Единственный.

три стороны одного треугольника равны соответственно трем сторонам другого треугольника, такие треугольники равны.

Когда, любые;

Любые, то;

Если, то.

высоты двух треугольников равны, их площади относятся как основания.

Тогда и только тогда, когда;

Если, то;

Когда, если.

два угла одного треугольника соответственно равны двум углам другого, такие треугольники подобны.

Если, то;

Тогда и только тогда, когда;

Когда, если.

точка срединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Единственная;

Некоторая;

Каждая.

прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, она пересекает только из двух других сторон.

Любая, если, единственную;

Если, то, одну;

Всякая, если, любую.

две хорды одной окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.

Когда, то;

Если, то;

Тогда, когда.

вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Единственный;

Любой;

Некоторый.

Логический анализ суждений.

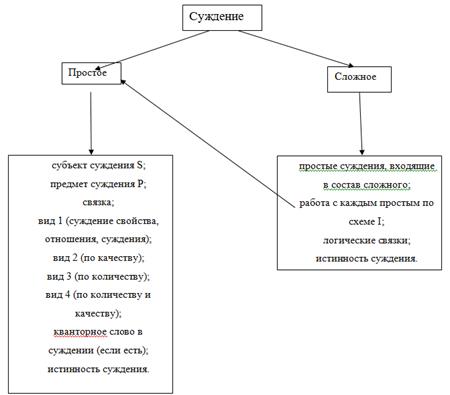
Прежде всего, необходимо представить общую схему анализа суждения.

1 . Определить каким является суждение: простым или сложным.

2. Работа со структурой суждения:

Простое суждение:

объект суждения S;

предмет суждения P;

связка;

вид 1 (суждение свойства, отношения, существования);

вид 2 (по качеству);

вид 3 (по количеству);

вид 4 (по количеству и качеству);

кванторное слово в суждении (если есть);

истинность суждения.

Сложное суждение:

простые суждения, входящие в состав сложного;

работа с каждым простым по схеме I;

логические связки;

истинность суждения.

Для наглядности представим данный анализ в виде схемы:

Рис. 11. Анализ суждения

Задание 22. Проанализируйте суждение: «Всякая неправильная дробь представима в виде смешанного числа».

Это простое суждение (I):

S - неправильная дробь;

P – смешанное число;

представима в виде;

суждение свойства;

утвердительное;

общее;

общеутвердительное;

всякая;

истинное суждение.

Задание 23. Проанализируйте суждение: «Средняя линия треугольника параллельная одной из его сторон и равна половине этой стороны».

Это сложное суждение (II):

b) Разбиваем на простые, работаем с каждым простым:

Средняя линия треугольника параллельная одной из его сторон (I):

S – средняя линия треугольника;

P – параллельная одной из его сторон;

согласование слов;

суждение свойства;

утвердительное;

общее;

общеутвердительное;

кванторного слова нет;

истинное суждение.

Средняя линия треугольника равна половине этой стороны (I):

S – средняя линия треугольника;

P – равна половине стороны;

согласование слов;

суждение свойства;

утвердительное;

общее;

общеутвердительное;

кванторного слова нет;

истинное суждение.

с) И – конъюнкция;

d) истинное суждение, так как оба простых суждения истинные.

Для анализа суждений в школьной курсе математики достаточно работы по этой схеме. Верное выполнение всех этапов потребует от учеников обращения к теории. Учитель может проводить работу по данной схеме на любом уроке, чтобы ученики научились работать с суждениями.

Простые суждения.

Задание 24. Проанализируйте суждение: «В любом треугольнике каждая сторона меньше суммы двух других сторон».

S - сторона;

P - сумма двух других сторон;

меньше;

суждение отношения;

утвердительное;

общее;

общеутвердительное;

любой;

истинное суждение.

Задание 25. Проанализируйте суждение: «Только некоторые остроугольные треугольники являются равносторонними».

S - остроугольные треугольники;

P - равносторонние;

являются;

утвердительное;

частное;

частноутвердительное;

некоторые;

истинное суждение.

В заключении необходимо отметить, что в ходе работы были получены следующие результаты:

составлены задачи, позволяющие совершенствовать процесс развития познавательных учебных действий через работу с суждениями

создана схема, позволяющая проводить анализ суждения;

проведена классификация суждений на основании проанализированной литературы.

На основе анализа методической, математической литературы нами были сделаны следующие выводы:

Развитие познавательных учебных действий - одна из основных целей обучения математики;

Суждение является основой любой науки, поэтому так важно научить школьников работать с ними;

Анализ суждений позволяет совершенствовать процесс формирования познавательных УУД.

Развитие познавательных учебных действий является основой для совершенствования всех остальных видов универсальных учебных действий.

Таким образом, математика представляет более наглядные возможности реализации идеи ФГОС об Универсальных учебных действиях.