Особенности изучения табличных случаев умножения и деления в начальной школе

Проанализируем решение этой задачи. В задаче рассматривалось множество, в котором 8 элементов. Оно разбивается на подмножества, в каждом из которых по 2 элемента, т. е. на равномощные подмножества (рис.1). Кроме того, они попарно не передаются. В задаче спрашивается, сколько таких подмножеств получилось. Таким образом, число 4, полученное в ответе, – это число двухэлементных подмножеств, на кот

орые разбито множество из 8 элементов.

Обратимся теперь к другой задаче: «12 карандашей раздали 3 ученикам поровну. Сколько карандашей получил каждый?»

Она также решается делением: 12:3=4 (карандаша). Но число 4 здесь выступает в другом смысле – как число элементов в каждом из трех равномощных непересекающихся подмножеств, на которые разбито множество, содержащее 12 элементов (рис.2).

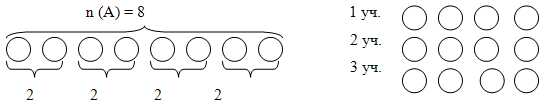
Рис. 1 Рис. 2

Иными словами, деление чисел связано с разбиением конечных множеств на равночисленные попарно непересекающиеся подмножества. При этом решаются две задачи: нахождение числа элементов в каждом подмножестве (деление на части) и нахождение числа таких подмножеств (деление по содержанию).

В общем виде частное целого неотрицательного числа а и натурального числа b определяется следующим образом:

Определение. Пусть а=n(А) и множество А разбито на попарно непересекающиеся равномощные подмножества.

Если b – число подмножеств в разбиении множества А, то частным чисел а и b называется число элементов каждого подмножества.

Если b – число элементов каждого подмножества в разбиении множества А, то частным чисел а и b называется число подмножеств в этом разбиении.

Действие, при помощи которого находят частное а:b, называется делением, число а – делимым, b – делителем.

Часто, чтобы проверить правильность выполнения действия деления, мы обращаемся к умножению. Почему? Очевидно, потому, что действия деления и умножения взаимосвязаны. Но какова эта связь?

Пусть а =n (А) и множество А разбито на b попарно непересекающихся равномощных подмножества А1, А2, ., Аb. Тогда с = a:b есть число элементов в каждом таком подмножестве, т. е.

с = a:b = n (A1) = n (A2) = … = n (Ab).

Так как по условию

A=A1 A2 . Аb,

то n(А) = n (A1A2 .Ab).

Но подмножества А1, А2, ., Аb попарно не пересекаются, значит, по определению суммы

n(A1A2 .Ab) = n(A1) + n(A2) +…+ n(Ab) = с + с + . + с.

b слагаемых

Согласно определению произведения сумма b слагаемых, каждое из которых равно c, есть произведение с·b.

Таким образом, установлено, что а = с·b, т. е. частным чисел а и b является такое число с, произведение которого и числа b равно а. К такому же выводу мы придем, если частное с = а:b будет числом подмножеств в разбиении множества А.

Таким образом, получаем второе определение частного:

Определение. Частным целого неотрицательного числа а и натурального числа b называется такое целое неотрицательное число с = а:b, произведение которого и числа b равно а.

Можно показать и наличие обратной связи, т. е. что из второго определения частного вытекает первое:

а:b = с а = с·b

Итак, во втором случае частное определено через произведение. Поэтому говорят, что деление есть действие, обратное умножению.

Всегда ли существует частное натуральных чисел a и b? Ответ на этот вопрос дает следующая теорема:

Теорема. Для того чтобы существовало частное двух натуральных чисел а и b, необходимо, чтобы bа.

Доказательство. Пусть частное натуральных чисел a и b существует, т. е. существует такое натуральное число с, что а = с·b. Для любого натурального числа с справедливо утверждение 1с. Умножим обе части этого неравенства на натуральное число b, получим b c·b. Поскольку с·b = а, то b а. Теорема доказана.

Чему равно частное а = 0 и натурального числа b? По определению это такое число а, которое удовлетворяет условию с·b = 0. Так как b ≠ 0, то равенство c·b = 0 будет выполняться при с = 0. Следовательно, 0:b = 0, если bN.

Теорема. Если частное натуральных чисел а и b существует, то оно единственно.

Рассмотрим теперь вопрос о невозможности деления целого неотрицательного числа на нуль.

Пусть даны числа а ≠ 0 и b = 0. Предположим, что частное чисел а и b существует. Тогда по определению частного существует такое целое неотрицательное число с, что а = с·0, отсюда а = 0. Пришли к противоречию с условием. Следовательно, частное чисел а ≠ 0 и b = 0 не существует.

Если a = 0 и b = 0, то из предложения, что частное таких чисел а и b существует, следует равенство 0 = с·0, истинное при любых значениях с, т. е. частным чисел а = 0 и b = 0 может быть любое число. Поэтому в математике считают, что деление нуля на нуль также невозможно.

В начальном курсе математики первоначальные представления о делении формируются на основе практических упражнений, связанных с разбиением, множества на попарно непересекающиеся равномощные подмножества, но без введения соответствующей терминологии и символики. Главным средством раскрытия этого понятия деления является решение простых задач.

Определение деления как действия, обратного умножению, в явном виде не дается. Взаимосвязь деления и умножения устанавливается при изучении темы «Нахождение неизвестного множителя», где, по существу, происходит обобщение двух смыслов частного, имеющих место при его теоретико-множественной трактовке.

Методика изучения табличных случаев умножения и деления

Тема «Умножение и деление чисел в пределах 100» является одной из основных тем начального курса математики. Изучается она во 2-м и 3-м классе.

Знанию таблицы умножения всегда придавали большое значение. Современная методика требует, чтобы дети не только знали таблицу умножения, но и поняли принципы составления таблицы, дающие возможность находить любое произведение. Поэтому ученик должен не только выучить и запомнить результаты табличного умножения, но и уметь при необходимости вычислять результаты самым кратчайшим способом.