Интеграл Лебега-Стилтьеса

Если же , но их общее значение отлично от ("устранимый разрыв"), то, наоборот, включим в число точек деления; пусть . Если dth=35 height=23 src="images/referats/3141/image006.png">имеет, например, разрыв в точке справа, то, как и только что, составим две суммы и , разнящиеся лишь выбором : для точка взята произвольно между и , а для в качестве взята . По-прежнему имеем (29), интеграл рассуждение завершается аналогично.

Упражнения 3) и 4) проливают свет на тот факт, о котором говорилось в конце п.4.

Пусть непрерывна, а имеет ограниченное изменение в промежутке .

Опираясь на оценку (25), доказать непрерывность интеграла Стилтьеса

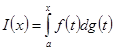
по переменному верхнему пределу в точке , где функция непрерывна.

Заключение сразу вытекает из неравенства

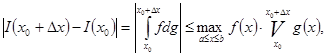
если принять во внимание, что в точке должна быть непрерывна и вариация .

Если есть класс непрерывных в промежутке функций, а - класс функций с ограниченным изменением в этом промежутке, то, как известно, каждая функция одного класса, интегрируема по каждой функции другого класса. Доказать, что ни один, ни другой из этих классов не может быть расширен с сохранением упомянутого свойства.

Это, ввиду 4), почти очевидно относительно класса . Действительно, если функция имеет точку разрыва , то она заведомо не интегрируема, например, по функции с ограниченным изменением , имеющей ту же точку разрыва.

Пусть теперь в промежутке имеет бесконечное полное изменение; в этом предположении построим такую непрерывную функцию , для которой интеграл (30) не существует.

Если разделить промежуток пополам, то хоть в одной из половин полное изменение функции тоже будет бесконечно; разделим эту половину снова пополам интеграл т.д. По этому методу определится некоторая точка , в каждой окрестности которой не имеет ограниченного изменения. Для простоты пусть .

В таком случае легко построить последовательность возрастающих интеграл стремящихся к значений :

так, чтобы ряд

расходился. Для этого ряда затем можно подобрать такую последовательность стремящихся к 0 чисел , чтобы и ряд

(31)

все же расходился. Теперь определим функцию , полагая

а в промежутках считая линейной:

Очевидно, будет непрерывна. В то же время, ввиду расходимости ряда (31), при и

так что интеграл от по действительно не существует.

Доказанное утверждение можно сформулировать и так: если интеграл Стилтьеса (30) для данной функции существует по любой из , то необходимо принадлежит ; аналогично, если этот интеграл по данной функции существует для любой из , то необходимо принадлежит .

 Скачать реферат