Интеграл Лебега-Стилтьеса

Если, как обычно, обозначить через колебание функции в промежутке , так что

для

то, применяя оценку (25) к каждому интегралу в отдельности, будем иметь

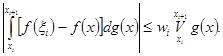
Если промежуток раздроблен на столь мелкие части, что все , где - произвольное наперед взятое число, то заключаем, что

(26)

Эти оценки будут нами использованы в следующем пункте.

2.11 Предельный переход под знаком интеграла Стилтьеса

Пусть функции непрерывны в промежутке и при равномерно стремятся к предельной функции

(очевидно, также непрерывной), а - функция с ограниченным изменением. Тогда

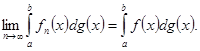
Доказательство: По заданному найдется такое , что при будет для всех

Тогда, в силу (25), для

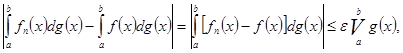
что, ввиду произвольности , и доказывает теорему.

Пусть теперь функция непрерывна в промежутке , а функции - все с ограниченным изменением в этом промежутке. Если полные изменения этих функций в их совокупности ограничены:

и при стремятся к предельной функции

То

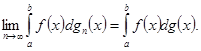
Доказательство:

Прежде всего, убедимся в том, что предельная функция сама также будет иметь ограниченное изменение. Разложив промежуток произвольным образом на части точками

будем иметь (при любом )

Переходя к пределу здесь при , получим

откуда и

Составим суммы Стилтьеса

Если предположить, что промежуток при этом разложен на столь мелкие части, что колебание функции в каждой из них будет уже меньше произвольного наперед взятого числа , то в силу оценки (26), при всех

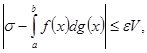(27)

С другой стороны, если разбиение, выбранное под указанным условием, фиксировать, то, очевидно, при , так что найдется такое , что для будет

. (28)

Тогда для тех же значений будем иметь, в силу (27) и (28),

откуда, ввиду произвольности , и следует требуемое заключение.

2.12. Примеры и дополнения

Предполагая функцию монотонно возрастающей в строгом смысле, можно доказать относительно числа , фигурирующего в формуле (24), более точное утверждение:

Действительно, обозначив через и наименьшее и наибольшее значения функции в промежутке и считая , легко найдем такую часть этого промежутка, в которой границами служат числа и , так что

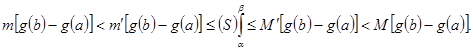
Написав для промежутков и неравенства вида (23) интеграл складывая их с предыдущими, получим взамен (23) более точные неравенства:

 Скачать реферат