Управление запасами

(3.24)

и из четырех ближайших точек с целочисленными координатами выбрать дающую наилучший результат. Сравнение должно проводиться по затратам в единицу времени

(3.25)

Преобразуем систему (2.14). подставив второе уравнение в первое и возведя в квадрат

обе части равенства, имеем

,

или

.

Таким образом, оптимальный набор дается условиями

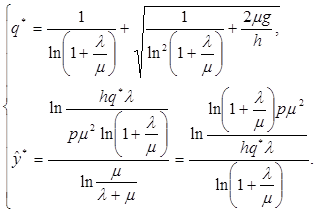(3.26)

В качестве приближенного решения можно использовать результат расчета q по средней интенсивности спроса с последующим вычислением согласно уравнению (2.14). в нашем случае соответствующие формулы примут вид

(3.27)

o Пример 5. Определение прироста затрат, связанного с отходом от строгой оптимальности

Положим, µ = 2, λ = 0,5, h = 2, g = 25, p = 70. При этих значениях параметров расчет по формулам (3.26) дает q = 12,90 и . Суммарные затраты в единицу времени составляют 40,03.

Приближенный расчет в соответствии (3.27) дает q = 7,06 и ; при этом сумма затрат достигает 42,9. Таким образом, разница в затратах, подсчитываемых согласно (3.25) для обоих вариантов вычислений , сравнительно невелика.

4. Динамическая модель управления запасами

Рассмотрим предприятие, которое изготовляет партиями некоторые изделия. Оно состоит из производственных цехов и склада для хранения готовой продукции. Предположим, что предприятие получило заказы на продукцию на n месяцев (этапов) вперед. Эти заказы необходимо полностью и своевременно выполнять (дефицит не допускается). Для разных этапов спрос не одинаков, кроме того, на экономические показатели производства влияют размеры изготовляемых партий продукции. Поэтому предприятию иногда бывает выгодно производить в течение месяца продукцию в объеме, превышающем спрос в пределах этого этапа, и хранить запасы «лишней» продукции, используя их для удовлетворения последующего спроса. Продолжительность изготовления партии изделий будем считать пренебрежимо малой (однако это требование может быть изменено в соответствии с особенностями технологического процесса). Цель предприятия – выработать такую программу производства, которая обеспечила бы минимальные затраты на изготовление и хранения продукции.

Введем обозначения:

xt – число изделий, изготовленных в t-м месяце (этапе);

yt – уровень запасов на конец t-го месяца;

dt – спрос на изделие в t-м месяце;

ft(xt, yt) – затраты на производство и хранение изделий в t-м месяце.

Соотношение материального базиса примет вид

(4.1)

т.е уровень запасов на конец t-го этапа равен сумме уровня запасов на начало t-го и объема производства на t-м этапе за вычетом спроса на t-м этапе.

Данное балансовое соотношение можно записать и в другом виде:

(4.2)

Наша задача состоит в том, чтобы составить такой план производства

X = (x1, …,xn), или, что тоже самое, найти такой план хранения запасов Y = (y1, …,yn), который обеспечил бы минимальные суммарные затраты предприятия

(4.3)

за весь плановый период.

Введем ограничения на переменные xt, yt. Будем считать объемы производства и уровни хранения на каждом этапе неотрицательными и целочисленными величинами. Кроме того, предположим, что уровни запасов к началу первого этапа y0 и к концу последнего yn заранее известны.

Решим сформулированную задачу методом динамического программирования. В качестве параметра состояния ζ примем уровень запасов на конец k-го этапа

. (4.4)

Функцию составления определим как минимальные затраты за первые k месяцев, т.е.

. (4.5)

Здесь абсолютный минимум берется по всем значениям x1, …,xk, удовлетворяющим балансовым уравнениям:

(4.6)

(4.7)

При k = 1 соотношение (4.7) примет вид

(4.8)

или

. (4.9)

Тогда с учетом (4.4) и (4.9) функция состояния

, (4.10)

причем если не видно никаких ограничений на объем складских помещений и производственную мощность предприятия, то

,

. (4.11)

Это связано с тем обстоятельством, что если иметь на конец 1-го этапа запас изделий в качестве , то, ничего не изготовляя в течение всего планового периода, а только удовлетворяя спрос, можно выйти на уровень запасов yn в конце n-го месяца. В то же время если уровень запасов на начало 1-го этапа равен y0, то, изготовив в 1-м месяце изделий в количестве и не производя ничего на последних этапах, получим тот же запас yn в конце планового периода. Если же на 1-м этапе предприятие может вместить готовой продукции не более М1 изделий, а мощности предприятия не позволяют произвести более N1 изделий, то

,

. (4.12)

Получим рекуррентное соотношение динамического программирования в модели управления запасами при любом k = 2, …,n.

Запишем функцию состояния (4.5) в виде

. (4.13)

Здесь, как уже было сказано выше, все переменные связаны балансовыми уравнениями

. (4.14)

В связи с тем что величина запаса yk-1 к концу (k – 1)-го планового этапа с учетом (4.7) равна , имеем следующее рекуррентное соотношение динамической модели управления запасами:

 Скачать реферат