Разностные схемы для уравнения переноса на неравномерных сетках

Таблица 18. Численное решение уравнения переноса с постоянными коэффициентами Трехточечная схема с весом Метод прогонки

Текст программы смотри в приложении 6

3.3.3 Схема “прямоугольник”

1. p>0 разностная схема правая имеет вид

2. p<0 разностная схема левая имеет вид

3.3.4 Схема со сглаживанием

Разностная схема имеет вид

1. p>0

2. p<0

Схема сводится к стандартному виду и решается методом прогонки.

3.3.5 Схема прямоугольник со сглаживанием

1.p>0

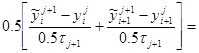
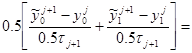
2. p<0

3.3.6 “Шахматная” схема

Имеем схему с весом

1. p>0

2. p<0

Параметр управляет реализацией схемы. При =0 и

(i+j)- четном решаем по явной схеме, при =1 и

(i+j)- нечетном решаем по неявной схеме явно. В целом схема реализуется явно.

Заключение

Теория разностных схем является самостоятельным разделом вычислительной математики, где изучаются методы приближенного решения дифференциальных уравнений путем замены их конечно –разностными уравнениями (разностными схемами).

Конечно –разностный метод (метод сеток) –один из мощных достаточно универсальных методов современной вычислительной математики. Этот метод относится к классу машинных методов решения широкого круга задач для дифференциальных уравнений.

В дипломной работе рассмотрены “явные” и неявные разностные методы решения для одномерного уравнения переноса с переменными коэффициентами и для одномерного уравнения переноса с постоянными коэффициентами на неравномерных сетках. Использованы такие разностные схемы, как схема бегущего счета, трехточечная схема с весом, центрально –разностная схема, схема “прямоугольник”, схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема.

 Скачать реферат