Пакет программ Майкрософт, как эффективное средство эконометрического анализа

Для значимых частных коэффициентов корреляции можно построить с заданной надёжностью г интервальную оценку сmin ≤ с ≤ сmax с помощью Z-преобразования Фишера:

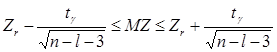
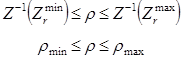
Алгоритм п

остроения интервальной оценки для частного генерального коэффициента корреляции такой же, как и для парного; единственное отличие заключается в расчёте ДZ :

,

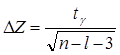где l – порядок частного коэффициента корреляции, совпадающий с количеством фиксируемых переменных случайных величин (в нашем случае l=3), а n – количество наблюдений.

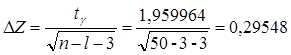
Построим с надёжностью г=0,95 и с учётом найденного доверительные интервалы для всех значимых частных коэффициентов корреляции, полученных нами. Расчёты представим в виде таблицы 11.

Таблица 11

Расчёт доверительных интервалов для частных генеральных коэффициентов корреляции исследуемых экономических показателей с надёжностью г=0,95

Таким образом, доверительные интервалы с надёжностью г=0,95 для всех значимых частных генеральных коэффициентов корреляции выглядят следующим образом:

P(0,23543867≤≤ 0,680954)=0,95

P(-0,707488≤≤ -0,283226)=0,95

Теперь построим таблицу сравнения выборочных парных и частных коэффициентов корреляции для всех переменных.

Сравнение парных и частных коэффициентов играет важную роль в выявлении механизмов воздействия переменных друг на друга.

Таким образом, если оказывается, что парный коэффициент корреляции между двумя переменными по модулю больше соответствующего частного, то остальные переменные усиливают связь между этими двумя признаками. Соответственно, если парный коэффициент корреляции между двумя переменными по абсолютной величине меньше частного, то остальные признаки ослабляют связь между рассматриваемыми двумя.

Таблица 12

Таблица сравнения выборочных оценок парных и частных коэффициентов корреляции пар исследуемых показателей с выделением значимых коэффициентов (при б=0,05)

По полученным данным можно сделать следующие выводы.

Значимые корреляционные зависимости, полученные на этапе расчёта парных коэффициентов корреляции, подтвердились и при вычислении частных коэффициентов корреляции только для связей между рентабельностью и фондоотдачей, и удельным весом рабочих в составе ППП и оборачиваемостью нормируемых оборотных средств. При этом выявлены следующие механизмы воздействия переменных друг на друга:

1. Прямая связь между рентабельностью и фондоотдачей достаточно тесная и значимая, при этом частный коэффициент по модулю немного меньше парного. Следовательно, остальные переменные, включённые в корреляционную модель (Х5 - удельный вес рабочих в составе ППП, Х7 - коэффициент сменности оборудования и X15 – оборачиваемость нормируемых оборотных средств) ослабляют взаимосвязь между указанными факторными признаками.

2. Между факторными признаками X5 - удельным весом рабочих в составе ППП и Х15 - оборачиваемость нормируемых оборотных средств также существует значимая обратная корреляционная связь. Её усиливают переменные, включенные в корреляционную модель, так как парный коэффициент по абсолютному значению больше частного.

 Скачать реферат