Пакет программ Майкрософт, как эффективное средство эконометрического анализа

В регрессионной статистике указываются множественный коэффициент корреляции (Множественный R) и детерминации (R-квадрат) между Y и массивом факторных признаков (что совпадает с полученными ранее значениями в корреляционном анализе)

Средняя часть таблицы (Дисперсионный анализ) необходима для проверки значимости уравнения регрессии.

Нижняя часть таблицы – точ

ечные оценки bi генеральных коэффициентов регрессии вi, проверка их значимости и интервальная оценка.

Оценка вектора коэффициентов b (столбец Коэффициенты):

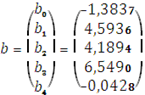
Тогда оценка уравнения регрессии имеет вид:

Необходимо проверить значимость уравнения регрессии и полученных коэффициентов регрессии.

Проверим на уровне б=0,05 значимость уравнения регрессии, т.е. гипотезу H0: в1=в2=в3=…=вk=0. Для этого рассчитывается наблюдаемое значение F-статистики:

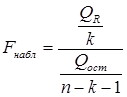
Excel выдаёт это в результатах дисперсионного анализа:

QR=527,4296; Qост=1109,8673 =>

В столбце F указывается значение Fнабл.

По таблицам F-распределения или с помощью встроенной статистической функции FРАСПОБР для уровня значимости б=0,05 и числа степеней свободы числителя н1=k=4 и знаменателя н2=n-k-1=45 находим критическое значение F-статистики, равное

Fкр = 2,578739184

Так как наблюдаемое значение F-статистики превосходит ее критическое значение 8,1957 > 2,7587, то гипотеза о равенстве вектора коэффициентов отвергается с вероятностью ошибки, равной 0,05. Следовательно, хотя бы один элемент вектора в=(в1,в2,в3,в4)T значимо отличается от нуля.

Проверим значимость отдельных коэффициентов уравнения регрессии, т.е. гипотезу .

Проверку значимости регрессионных коэффициентов проводят на основе t-статистики для уровня значимости .

Наблюдаемые значения t-статистик указаны в таблице результатов в столбце t-статистика.

Их необходимо сравнить с критическим значением tкр, найденным для уровня значимости б=0,05 и числа степеней свободы н=n – k - 1.

Для этого используем встроенную статистическую функцию Excel СТЬЮДРАСПОБР, введя в предложенное меню вероятность б=0,05 и число степеней свободы н= n–k-1=50-4-1=45. (Можно найти значения tкр по таблицам математической статистики.

Получаем tкр= 2,014103359.

Для наблюдаемое значение t-статистики меньше критического по модулю 2,0141>|-0,0872|, 2,0141>|0,2630|, 2,0141>|0,7300|, 2,0141>|-1,6629|.

Следовательно, гипотеза о равенстве нулю этих коэффициентов не отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты незначимы.

Для наблюдаемое значение t-статистики больше критического значения по модулю |3,7658|>2,0141, следовательно, гипотеза H0 отвергается, т.е. - значим.

Значимость регрессионных коэффициентов проверяют и следующие столбцы результирующей таблицы:

Столбец p-значение показывает значимость параметров модели граничным 5%-ым уровнем, т.е. если p≤0,05, то соответствующий коэффициент считается значимым, если p>0,05, то незначимым.

И последние столбцы – нижние 95% и верхние 95% и нижние 98% и верхние 98% - это интервальные оценки регрессионных коэффициентов с заданными уровнями надёжности для г=0,95 (выдаётся всегда) и г=0,98 (выдаётся при установке соответствующей дополнительной надёжности).

Если нижние и верхние границы имеют одинаковый знак (ноль не входит в доверительный интервал), то соответствующий коэффициент регрессии считается значимым, в противном случае – незначимым

Как видно из таблицы, для коэффициента в3 p-значение p=0,0005<0,05 и доверительные интервалы не включают ноль, т.е. по всем проверочным критериям этот коэффициент является значимым.

Согласно алгоритму пошагового регрессионного анализа с исключением незначимых регрессоров, на следующем этапе необходимо исключить из рассмотрения переменную, имеющую незначимый коэффициент регрессии.

В случае, когда при оценке регрессии выявлено несколько незначимых коэффициентов, первым из уравнения регрессии исключается регрессор, для которого t-статистика () минимальна по модулю. По этому принципу на следующем этапе необходимо исключить переменную Х5 , имеющую незначимый коэффициент регрессии в2

II ЭТАП РЕГРЕССИОННОГО АНАЛИЗА.

В модель включены факторные признаки X7, X10, X15, исключён X5.

 Скачать реферат