Пакет программ Майкрософт, как эффективное средство эконометрического анализа

Оценка коэффициентов в случае двух объясняющих переменных имеет вид:

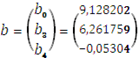
а уравнение регрессии имеет вид:

Проверим на уровне б=0,05 значимость уравнения регрессии, т.е. гипотезу H0: в3=в4=0. Для этого в результатах дисперсионного анализа находи

м наблюдаемое значение F-статистики Fнабл=10,6274.

С помощью встроенной статистической функции FРАСПОБР или по таблицам F-распределения для уровня значимости б=0,05 и числа степеней свободы числителя н1=k=2 и знаменателя н1=n-k-1=50-2-1=47 находим критическое значение F-статистики, равное

Fкр = 3,195056281

Так как наблюдаемое значение F-статистики превосходит ее критическое значение 10,6274> 3,19505, то гипотеза о равенстве вектора коэффициентов отвергается с вероятностью ошибки, равной 0,05. Следовательно, хотя бы один элемент вектора в=(в3,в4)T значимо отличается от нуля.

Проверим значимость отдельных коэффициентов уравнения регрессии, т.е. гипотезу H0:вi=0, i=3,4.

Наблюдаемые значения t-статистик указаны в таблице результатов в столбце t-статистика.

Их необходимо сравнить с критическим значением tкр, найденным для уровня значимости б=0,05 и числа степеней свободы н=n – k - 1.

Для этого используем встроенную статистическую функцию Excel СТЬЮДРАСПОБР, введя в предложенное меню вероятность б=0,05 и число степеней свободы н= n–k-1=50-2-1=47. (Можно найти значения tкр по таблицам математической статистики).

Получаем tкр= 2,01174048.

Для всех рассматриваемых коэффициентов в0,в3,в4 наблюдаемое значение t-статистики больше критического по модулю

|2,710886|>2,01174048, |3,746677|>2,01174048, |-2,71665|>2,01174048

Следовательно, гипотеза о равенстве нулю коэффициентов отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты значимы.

Эту гипотезу так же подтверждают p-значения:

0,05 >

и доверительные интервалы не включают ноль, т.е. по всем проверочным критериям эти коэффициенты являются значимыми.

Т.к. в данном случае все коэффициенты оказались значимыми, процесс исключения переменных прекращается

Окончательная оценка регрессии со значимыми коэффициентами имеет вид:

Для значимых коэффициентов регрессии можно найти с заданной доверительной вероятностью г интервальные оценки.

Таким образом, интервальные оценки значимых генеральных коэффициентов регрессии имеют вид:

Интерпретация результатов

Величина R2 характеризует долю общей дисперсии зависимой переменной, обусловленную воздействием объясняющих переменных. Т.е. около 31,14% вариации рентабельности (Y) объясняется вариацией фондоотдача (X10) и оборачиваемостью нормируемых оборотных средств (X15), а 68,86% вариации вызвано воздействием неучтенных в модели и случайных факторов. Таким образом, можно утверждать, что модель слабо отражает исследуемый процесс.

Коэффициент регрессии показывает среднюю величину изменения зависимой переменной Y при изменении объясняющей переменной X на единицу собственного изменения. Знак при коэффициенте указывает направление этого изменения.

Коэффициент регрессии при X10 показывает, что при росте фондоотдачи на единицу рентабельность Y в среднем увеличится на 6,2618 единиц. Построенная выше интервальная оценка показывает, что с вероятностью 0,95 при росте оборачиваемости ненормируемых оборотных средств на единицу увеличение рентабельности будет в пределах от 2,90 до 9,62 единиц.

Аналогично, коэффициент при X15 свидетельствует о том, что при росте оборачиваемости нормируемых оборотных средств на единицу рентабельность в среднем уменьшается на 0,0530 единиц, а с вероятностью 0,95 при росте оборачиваемости нормируемых оборотных средств на единицу уменьшение рентабельности будет в пределах от 0,01376 до 0,09232 единиц.

3.3 Сравнение исходных данных с рассчитанными по уравнению регрессии

Таблица 15

 Скачать реферат