Пакет программ Майкрософт, как эффективное средство эконометрического анализа

Итак, полученные результаты корреляционного анализа, показавшие, что показатель Y3 – рентабельность имеет умеренную связь с многомерным массивом факторных признаков, позволяют перейти ко второму этапу статистического исследования – построению регрессионной модели.

3. Регрессионный анализ экономических показателей

После того как с помощью корреляционного анализа выявлено наличие с

татистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель Y и аргументы X1, X2, X3 , . Xk, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.

Наиболее часто используется множественная линейная модель регрессионного анализа, уравнение которой имеет вид:

для всех i=1,2,…n, или в матричной форме: ,

Где

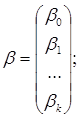
Исследуем на основе линейной регрессионной модели зависимость рентабельности (Y) от удельного веса рабочих в составе ППП (Х5), коэффициента сменности оборудования (Х7) , фондоотдачи (X10) и оборачиваемости нормируемых оборотных средств (X15).

3.1 Проверка исходных данных на мультиколлинеарность

Одним из основных препятствий эффективного применения множественного регрессионного анализа является мультиколлинеарность. Она возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными X1, X2, X3 , . Xk. В результате мультиколлинеарности матрица парных коэффициентов корреляции становится слабообусловленной, близкой к вырожденной.

Точных количественных критериев для определения наличия или отсутствия мультиколлинеарности не существует. Однако существуют некоторые рекомендации по выявлению этого негативного явления, на которые следует обратить внимание. На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше 0,8 , т.е. | rij | > 0,8 , то считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включать только один из показателей Xi или Xj (как правило, тот, который имеет наибольшую связь с Y).

Прежде, чем переходить к построению регрессионной модели, необходимо проверить объясняющие переменные на наличие мультиколлинеарности. Для этого рассмотрим матрицу парных коэффициентов корреляции между факторными признаками Xi.

Таблица 14

Матрица парных коэффициентов корреляции факторных признаков

Поскольку значения коэффициентов корреляции для всех пар объясняющих переменных не превышают по модулю 0,8, то нет необходимости сокращать набор объясняющих переменных.

3.2 Построение регрессионной модели и её интерпретация

Будем использовать алгоритм пошагового регрессионного анализа с последовательным исключением незначимых регрессоров, пока все входящие в регрессионную модель факторы не будут иметь значимые коэффициенты.

Построение и оценка регрессионной модели осуществляется в Excel с помощью модуля регрессии пакета анализа данных.

в менюOffice 2007

ДАННЫЕ

Анализ данных (DataAnalysis)

Регрессия (Regression)

Задаем нужные параметры.

I ЭТАП РЕГРЕССИОННОГО АНАЛИЗА.

В модель включены все факторные признаки (X5, X7, X10 , X15).

 Скачать реферат