Пакет программ Майкрософт, как эффективное средство эконометрического анализа

3. Для связи рентабельности (Y) с удельным весом рабочих в составе ППП (Х5), а также рентабельности и коэффициента сменности оборудования (Х7) характерна следующая ситуация: обе связи незначимы, являются прямыми, воздействие других переменных значительно усиливает эти взаимосвязи.

4. Парный коэффициент корреляции для связи X5X7 значим, но его частный коэффициент незначим, то есть значимость

этой прямой корреляционной связи не подтвердилась. В тоже время, ее усиливают переменные, включенные в корреляционную модель.

5. Аналогичная ситуация происходит со связями рентабельности (Y) с оборачиваемостью нормируемых оборотных средств (X15) и коэффициента сменности оборудования (X7) также с оборачиваемостью нормируемых оборотных средств: парный коэффициент значим, взаимосвязи обратные, и их усиливает переменные, включенные в модель.

6. Единственная обратная взаимосвязь, которая ослабляется остальными переменными – это связь между коэффициентом сменности оборудования (X7) и фондоотдачей (Х10), так как значение частного коэффициента превышает значение парного по модулю. Но эта взаимосвязь незначима.

2.3 Расчёт множественных коэффициентов корреляции

Множественные коэффициенты корреляции служат мерой связи одной переменной с совместным действием всех остальных показателей.

Вычислим точечные оценки множественных коэффициентов корреляции. Множественный коэффициент корреляции, например, для 1-го показателя Y вычисляется по формуле:

где |R| - определитель корреляционной матрицы R;

Rii – алгебраическое дополнение элемента rii корреляционной матрицы R.

Все алгебраические дополнения Rii были найдены в п.2.2 на этапе расчёта частных коэффициентов корреляции, поэтому осталось вычислить только определитель самой корреляционной матрицы.

Чтобы найти определитель корреляционной матрицы, воспользуемся встроенной математической функцией ExcelМОПРЕД.

Получим|R| =0,327084571.

;

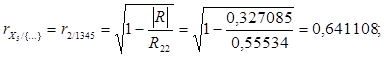
Множественный коэффициент детерминации R2i/{ }) (и его выборочная оценка r2i/{ }) показывает долю дисперсии рассматриваемой случайной величины, обусловленную влиянием остальных переменных, включённых в корреляционную модель.

Соответственно (1- R2i/{ }) показывает долю остаточной дисперсии данной случайной величины, обусловленную влиянием других, не включённых в исследуемую модель факторов.

Множественные коэффициенты детерминации получаются возведением соответствующих множественных коэффициентов корреляции в квадрат (таб. 13).

Проверим значимость полученных множественных коэффициентов корреляции и детерминации.

Проверка значимости, т.е. гипотезы о равенстве нулю соответствующего множественного коэффициента корреляции, осуществляется с помощью статистики:

,

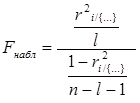где l – порядок множественного коэффициента корреляции, совпадающий с количеством фиксируемых переменных случайных величин (в нашем случае l=4, например, ), а n – количество наблюдений.

Произведя расчёты, получим (таб.13).

Для определения значимости множественных коэффициентов корреляции и детерминации нужно найти критическое значение F-распределения для заданного уровня значимости б и числа степеней свободы числителя н1=l и знаменателя н2=n-l-1.

Для определения Fкр можно воспользоваться встроенной функцией Excel:

ВСТАВКА (Office 2003) или ФОРМУЛЫ (Office 2007)

f(x) Функция

Статистические

FРАСПОБР,

введя в предложенное меню вероятность б=0,05 и число степеней свободы н1=l=4 и н2=n-l-1=50-4-1=45.

Можно найти значения Fкр по таблицам математической статистики.

Получаем Fкр(0,05; 4; 45)= 2,578739184.

Таблица 13

Множественные коэффициенты корреляции и детерминации исследуемых показателей с выделением значимых коэффициентов (на уровне значимости б=0,05)

Если наблюдаемое значение F-статистики превосходит ее критическое значение Fкр=2,578739184, то гипотеза о равенстве нулю соответствующего множественного коэффициента корреляции отвергается с вероятностью ошибки, равной 0,05. Следовательно, у нас все коэффициенты значимо отличаются от нуля.

Полученные данные позволяют сделать следующие выводы.

Множественный коэффициент корреляции = 0,5675688 значим и имеет достаточно высокое значение, что говорит о том, показатель Y – рентабельность имеет умеренную связь с многомерным массивом факторных признаков X5 – удельный вес рабочих в составе ППП, X7 – коэффициент сменности оборудования, X10 - фондоотдача и X15 – оборачиваемость нормируемых оборотных средств. Это даёт основание для проведения дальнейшего регрессионного анализа.

Множественный коэффициент детерминации r2Y/{ }=0,3221344 показывает, что 32,21% доли дисперсии Y – объёма промышленной продукции, обусловлены изменениями факторных признаков.

Факторные признаки также являются значимыми, несмотря на то, что у Х7 и Х10 всего 22,63% и 27,80% доля дисперсии соответственно обусловлены изменениями факторных признаков. Более тесная связь с другими переменными наблюдается у Х5 и Х15, у которых 41,10% и 44,15% доли дисперсии обусловлены изменениями остальными рассматриваемыми признаками, а остальное факторами, которые не включены в изучаемую модель.

 Скачать реферат