Пакет программ Майкрософт, как эффективное средство эконометрического анализа

Оценка коэффициентов в случае трех объясняющих переменных имеет вид:

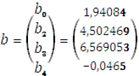
а уравнение регрессии имеет вид:

Проверим на уровне б=0,05 значимость уравнения регрессии, т.е. гипотезу H0: в2=в3=в4=0. Для этого в результатах дисперсионного анализа нах

одим наблюдаемое значение F-статистики Fнабл=7,251979.

С помощью встроенной статистической функции FРАСПОБР или по таблицам F-распределения для уровня значимости б=0,05 и числа степеней свободы числителя н1=k=3 и знаменателя н1=n-k-1=46 находим критическое значение F-статистики, равное

Fкр = 2,80684494

Так как наблюдаемое значение F-статистики превосходит ее критическое значение 7,251979 > 2,80684494, то гипотеза о равенстве вектора коэффициентов отвергается с вероятностью ошибки, равной 0,05. Следовательно, хотя бы один элемент вектора в=(в2,в3,в4)T значимо отличается от нуля.

Проверим значимость отдельных коэффициентов уравнения регрессии, т.е. гипотезу. H0:вi=0, i=2,3,4.

Наблюдаемые значения t-статистик указаны в таблице результатов в столбце t-статистика.

Их необходимо сравнить с критическим значением tкр, найденным для уровня значимости б=0,05 и числа степеней свободы н=n – k - 1.

Для этого используем встроенную статистическую функцию Excel СТЬЮДРАСПОБР, введя в предложенное меню вероятность б=0,05 и число степеней свободы н= n–k-1=50-3-1=46. (Можно найти значения tкр по таблицам математической статистики).

Получаем tкр= 2,012895567.

Для в3, в4 наблюдаемое значение t-статистики больше критического по модулю |3,819738|>2,012895567, |-2,19389|>2,012895567.

Следовательно, гипотеза о равенстве нулю этих коэффициентов отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты значимы.

Для в0, в2, наблюдаемое значение t-статистики меньше критического значения по модулю |0,204457|<2,012895567, |0,204457|<0,810241, следовательно, гипотеза H0 не отвергается, т.е. в0, в2 - незначимы.

Столбец p-значение показывает, что для коэффициентов в3, в4 p3= 0,000398559, p4= 0,03333, т.е они меньше 0,05, следовательно, данные коэффициенты значимы.

Для в0, в2, p0= 0,83889, p1= 0,42197, то есть по всем проверочным критериям эти коэффициенты незначимы.

Согласно алгоритму пошагового регрессионного анализа с исключением незначимых регрессоров, на следующем этапе необходимо исключить из рассмотрения переменную X7 (коэффициент сменности оборудования), имеющую незначимый коэффициент регрессии в2.

III ЭТАП РЕГРЕССИОННОГО АНАЛИЗА.

В модель включены факторные признаки X10, X15., исключён X5, Х7.

 Скачать реферат