Рассеяние рентгеновских лучей на молекулах фуллерена

Поверхность постоянной фазы первичной плоской монохроматической волны достигает центров рассеяния с различными координатами z ¹ 0 в разные моменты времени. Как следствие, начальная фаза волны, рассеянной атомом с координатой z ¹ 0 будет отставать от фазы волны, рассеянной атомом с координатой z = 0, на величину w Dt, где Dt = z / v, v – скорость распространения волны. Частота и длина

волны связаны соотношением

w = 2pv / l(3.35)

следовательно, сдвиг фазы рассеянной волны равняется -2pz / l или -kz.

С другой стороны, если координата j-го атома zj ¹ 0, разность хода относительно «нулевой» рассеянной волны дополнительно увеличивается на величину z cos(q). В результате, сдвиг фазы волны, рассеянной атомом с произвольными координатами (xj, yj, zj) в направлении, заданном углами q и Ф, равен

Djj = k { [xj cos(Ф) + yj sin(Ф)] sin(q) + zj cos(q) - zj}. (3.36)

Интенсивность рассеянных рентгеновских лучей, регистрируемая детектором, выражается следующей формулой:

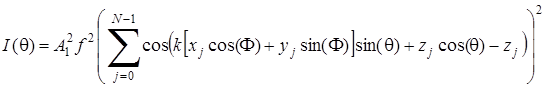(3.37)

3. Практическая часть

3.1. Псевдосимметрия

3.1.1. Поворотная псевдосимметрия дифракционных картин

Симметрией называется инвариантность физической или геометрической системы по отношению к различного рода преобразованиям.

Различные типы симметрии определяются преобразованиями, относительно которых инвариантна данная система. Существует симметрия трансляционная, поворотная, симметрия подобия и т.д.

Симметрия представляет собой одно из фундаментальных свойств Вселенной. Даже основные законы физики: сохранения энергии, импульса и момента импульса связаны с определенными симметрическими преобразованиями пространственно-временного континуума.

Конкретное преобразование, относительно которого инвариантна данная система, называется операцией симметрии. Множество точек, остающихся неподвижными при симметрическом преобразовании, образуют элемент симметрии. Например, если операцией симметрии является поворот, то соответствующим элементом симметрии будет ось, вокруг которой совершается поворот.

Симметрия конечных физических систем, элементы симметрии которых пересекаются хотя бы в одной точке, называется точечной. К точечной симметрии относятся инвариантность относительно поворота на определенный угол (поворотная симметрия), инвариантность относительно отражения в определенной плоскости (зеркальная симметрия), инвариантность относительно инверсии в заданной точке (инверсионная симметрия).

Симметрия подавляющего большинства физических объектов не является абсолютной. Это означает, что физическая или геометрическая система не полностью инвариантна относительно рассматриваемого преобразования.

Для количественного описания отклонений от точной симметрии используется функционал, называемый степенью инвариантности или коэффициентом псевдосимметрии.

Пусть какая-либо физическая характеристика исследуемого объекта описывается функцией точки . Этой функцией может быть массовая плотность, температура электрический потенциал, плотность электрического заряда и т.д. Нас симметрия данного объекта относительно преобразования, которое задано некоторой операцией . Тогда степень инвариантности определяется следующей формулой (4.1), где V – объем объекта. Под интегралом в числителе находится произведение функции на функцию того же объекта, подвергнутого преобразованию . Числитель называется сверткой функции относительно операции . В знаменателе стоит определенный интеграл по объему объекта от квадрата функции .

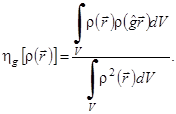(4.1)

Знаменатель формулы (4.1) служит нормировкой, поэтому величина функционала может изменяться от 0 до 1. Если рассматриваемая физическая система полностью инвариантна относительно операции , то коэффициент псевдосимметрии равен единице. Значение = 0 соответствует случаю, когда симметрия системы относительно операции полностью отсутствует.

Понятие степени инвариантности можно распространить и на описание симметрии углового распределения интенсивности рассеянных рентгеновских лучей. В первую очередь, нас интересует инвариантность дифракционных картин относительно поворота на определенный азимутальный угол вокруг точки, соответствующей полярному углу q = 0. Иначе говоря, целью исследования является поворотная симметрия углового распределения интенсивности рассеянных рентгеновских лучей, причем поворот осуществляется вокруг волнового вектора k0 первичного излучения.

Для изучения особенностей поворотной симметрии дифракционных картин можно адаптировать функционал общего вида (1). Исследуемой функцией в данном случае является угловое распределение интенсивности рассеянных рентгеновских лучей I(q, Ф), а операцией симметрии – поворот дифракционной картины на азимутальный угол a вокруг центральной точки картины с полярным углом q = 0. Таким образом, количественной характеристикой поворотной симметрии дифракционной картины является следующий функционал:

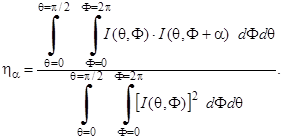(4.2)

Внутренние интегралы берутся по диапазону азимутального угла ФÎ [0, 2π], а внешние интегралы по диапазону полярного угла q Î [0, π/2].

Следует обратить внимание на некоторые важные особенности всех дифракционных картин. На рис.4.1. видно, что в центре полярной диаграммы находится центральный максимум интенсивности рассеянного излучения. Этот максимум имеет высокую симметрию, близкую к симметрии предельной группы С¥. В угловом распределении рассеянного излучения центральный максимум занимает некоторый интервал полярных углов q Î [0, qC]. Полуширина центрального максимума существенно зависит от длины волны рентгеновских лучей l и количества рассеивающих атомов.

Также весьма важно, что интенсивность центрального максимума значительно превышает интенсивность всех остальных точек двумерного угловом распределении рассеянного рентгеновского излучения. Напротив, с ростом полярного угла интенсивность рассеянного излучения в среднем резко падает. Это означает, что периферийная область дифракционной картины (область полярных углов превышающих некоторое значение qM) практически не влияет на величину коэффициента поворотной псевдосимметрии (4.2).

 Скачать реферат