Рассеяние рентгеновских лучей на молекулах фуллерена

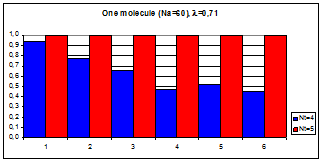
Рис.4.4. Гистограмма коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 0,71 Å на молекуле фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq

= 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.

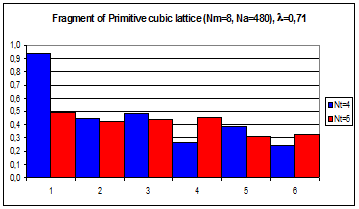
А

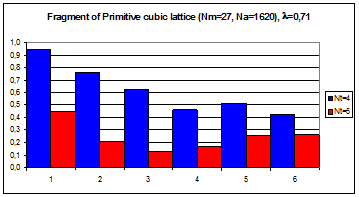
б

Рис.4.5. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 0,71 Å на фрагменте кубической примитивной решетки, в узлах которой расположены молекулы фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq = 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.

Число молекул фрагмента а) NМ = 8, б) NМ = 27.

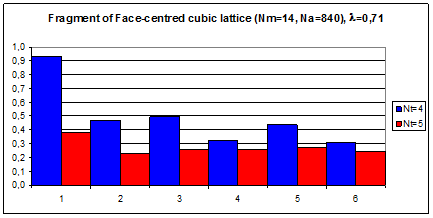
а

б

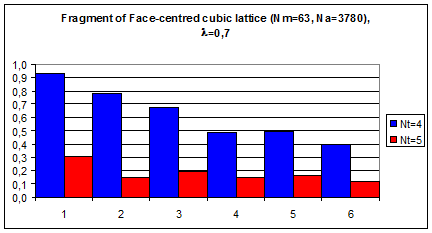
Рис.4.6. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 0,71 Å на фрагменте кубической гранецентрированной решетки, в узлах которой расположены молекулы фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq = 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.

Число молекул фрагмента а) NМ = 14, б) NМ = 63.

Сравнение рисунков 4.4. и 4.5, а также 4.4. и 4.6. ясно демонстрирует, что с увеличением количества молекул (и атомов) в кристаллическом фрагменте величина коэффициента поворотной псевдосимметрии 5-го порядка уменьшается во всех поддиапазонах полярного угла. Это объясняется тем, что кубические фрагменты структуры трансляционно упорядоченных молекул фуллерена не обладают поворотной симметрией 5-го порядка.

С другой стороны, на рис.4.4. - 4.6. видно, что с ростом количества молекул увеличивается коэффициент поворотной псевдосимметрии 4-го порядка из-за возрастания количества рассеивающих объектов, находящихся в узлах примитивной кубической кристаллической решетки. Таким образом, в дифракционных картинах точечная симметрия кристаллической решетки превалирует над точечная симметрией отдельных атомных кластеров, расположенных в узлах решетки, даже если все кластеры имеют одинаковую ориентацию.

Указанные тенденции наблюдаются на фрагментах как примитивной, так и гранецентрированной кубической кристаллической решетки.

Далее приводятся результаты аналогичных расчетов коэффициента поворотной псевдосимметрии для длины волны рентгеновского излучения l = 1,54 Å.

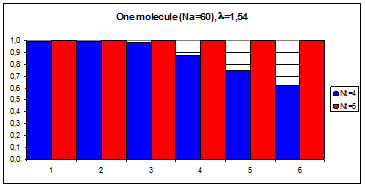
Рис.4.7. Гистограмма коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 1,54 Å на молекуле фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq = 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.

а

б

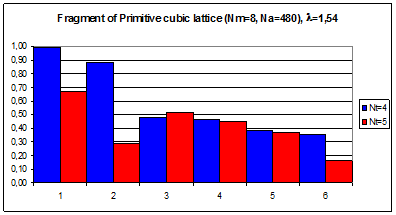
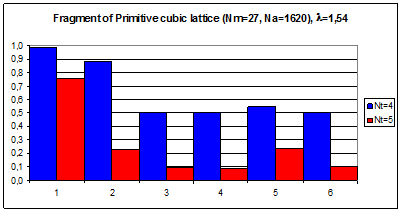
Рис.4.8. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 1,54 Å на фрагменте кубической примитивной решетки, в узлах которой расположены молекулы фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq = 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.

Число молекул фрагмента а) NМ = 8, б) NМ = 27.

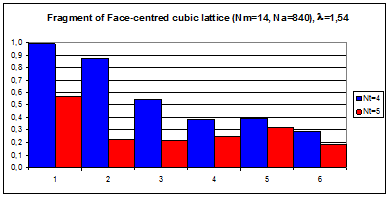
а

б

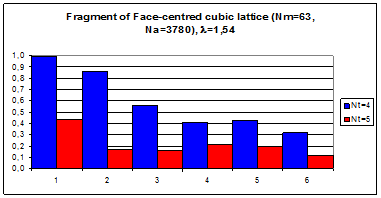
Рис.4.9. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны l = 0,71 Å на фрагменте кубической гранецентрированной решетки, в узлах которой расположены молекулы фуллерена С60.

По вертикали отложены значения степени инвариантности ha, по горизонтали – порядковые номера поддиапазонов полярного угла шириной dq = 15°. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны. Число молекул фрагмента а NМ = 14, б NМ = 63.

Из сравнения рисунков 4.7-4.9. следуют те же выводы о подавлении точечной симметрии атомных кластеров точечной симметрия кристаллической решетки с возрастанием количества атомов кристаллического фрагмента (количества кластеров, расположенных в узлах кристаллической решетки). Эти выводы подтверждаются расчетами для примитивной и гранецентрированной кубической кристаллической решетки.

4. Выводы

1. Разработан алгоритм и компьютерная программа расчета углового распределения интенсивности рентгеновского излучения, рассеянного фрагментом атомной структуры в условиях дифракции Фраунгофера.

2. С помощью программы выполнены расчеты дифракционных картин, полученных при рассеянии рентгеновских лучей разных длин волн на молекулах фуллерена и фрагментах кубических структур фуллеритов.

3. Проведены исследования поворотной псевдосимметрии дифракционных картин для вышеуказанных рассеивателей. Обнаружена тенденция подавления точечной симметрии отдельных молекул симметрией кристаллической решетки.

5. Список используемой литературы

1. Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А. Кристаллография. М.: Издательство Физико-математической литературы, 2000.496 с.

2. Иванов Б.Н. Законы физики. М.: Высшая школа, 1986.335 с.

3. Иванов А.И., Минькова Р.Д., Панаиоти Н.Н. физика 9 класс. Часть I. М.: 2002.128 с.

4. Мякишев Г.Я. Синяков А.З. Физика. Колебания и волны. М.: Дрофа, 2007.287 с.

5. Потапов М.К., Александров В.В., Пасиченко П.И. Алгебра и анализ элементарных функций. Справочное пособие. М.: АО «СТОЛЕТИЕ», 1996.736 с.

6. Чупрунов Е.В., Сафьянов., Головачев В.П., Фаддеев М.А., Хохлов А.Ф. Задачи по кристаллографии. М.: Издательство Физико-математической литературы 2003. 208 с.

7. Бытько Н.Д. Физика. ч.1 и 2. М.: Высшая школа. 1972.336 с.

8. Ф. Крауфорд. Волны. 1965г.529с.

9. Горелик Г.С. Колебания и волны. М.: Государственное издательство физико-математической литературы, 1959г.572с.

 Скачать реферат