Рассеяние рентгеновских лучей на молекулах фуллерена

Как уже было сказано ранее, рентгеновские лучи испускаются при торможении быстрых электронов в веществе и при переходах электронов с внешних электронных оболочек атома на внутренние (и дают линейчатый спектр). Детекторы, регистрирующие рентгеновские лучи базируются на свойствах рентгеновских лучей. Поэтому чаще всего в качестве детекторов используются: фотоэмульсии на пленке и пластинках, люмин

есцентные экраны, газонаполненные и полупроводниковые детекторы.

2.3. Дифракция волн

2.3.1. Дифракция и интерференция волн

Типичными волновыми эффектами являются явления интерференции и дифракции.

Первоначально дифракцией называлось отклонение распространения света от прямолинейного направления. Это открытие было сделано в 1665 году аббатом Франческо Гримальди и послужило основой для разработки волновой теории света. Дифракцией света представляла собой огибание светом контуров непрозрачных предметов и, как следствие этого, проникновение света в область геометрической тени.

После создания волновой теории выяснилось, что дифракция света является следствием явления интерференции волн, испущенных когерентными источниками, находящимися в различных точках пространства.

Волны называются когерентными, если разность их фаз остается постоянной с течением времени. Источниками когерентных волн являются когерентные колебания источников волн. Синусоидальные волны, частоты которых не изменяются с течением времени, являются всегда когерентными.

Когерентные волны, испущенные источниками, находящимися в различных точках, распространяются в пространстве без взаимодействия и образуют суммарное волновое поле. Строго говоря, сами волны не «складываются». Но если в какой-либо точке пространства находится регистрирующий прибор, то его чувствительный элемент будет приведен в колебательное движение под действием волн. Каждая волна действует независимо от других, и движение чувствительного элемента представляет собой сумму колебаний. Иначе говоря, в этом процессе складываются не

Рис. 3.1. Система двух источников и детектора. L – расстояние от первого источника до детектора, L’ – расстояние от второго источника до детектора, d – расстояние между источниками.

В качестве базового примера рассмотрим интерференцию волн, испускаемых двумя точечными когерентными источниками (см. рис.3.1). Частоты и начальные фазы колебаний источников совпадают. Источники находятся на определенном расстоянии d друг от друга. Детектор, регистрирующий интенсивность образованного волнового поля, располагается на расстоянии L от первого источника. Вид интерференционной картины зависит от геометрических параметров источников когерентных волн, от размерности пространства, в котором распространяются волны и т.д.

Рассмотрим функции волн, которые являются следствием колебаний, испускаемых двумя точечными когерентными источниками. Для этого пустим ось z так, как показано на рис.3.1. Тогда волновые функции будут выглядеть так:

(3.1)

Введём понятие разности хода волн. Для этого рассмотрим расстояния от источников до регистрирующего детектора L и L’. Расстояние между первым источником и детектором L отличается от расстояния между вторым источником и детектором L’ на величину t. Для того чтобы найти t рассмотрим прямоугольный треугольник, содержащий величины t и d. Тогда можно легко найти t, воспользовавшись функцией синуса:

(3.2)

Эта величина и будет называться разностью хода волн. А теперь помножим эту величину на волновое число k и получим величину, называемую разность фаз. Обозначим её, как ∆φ

(3.3)

Когда две волны «дойдут» до детектора функции (3.1) примут вид:

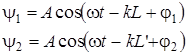(3.4)

Для того чтобы упростить закон, по которому будет колебаться детектор, занулим величину (–kL + j1) в функции x1(t). Величину L’ в функции x2(t) распишем её по функции (3.4). Путем несложных преобразований получаем, что

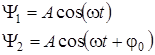(3.5)

где

(3.6)

Можно заметить, что соотношения (3.3) и (3.6) одинаковы. Ранее эта величина была определена, как разность фаз. Исходя из ранее сказанного, Соотношение (3.6) можно переписать следующим образом:

(3.7)

Теперь сложим функции (3.5).

(3.8)

Воспользовавшись методом комплексных амплитуд, мы получим соотношение для амплитуды суммарного колебания:

(3.9)

где φ0 определяется соотношением (3.3).

После того, как была найдена амплитуда суммарного колебания, можно найти интенсивность суммарного колебания, как квадрат амплитуды:

(3.10)

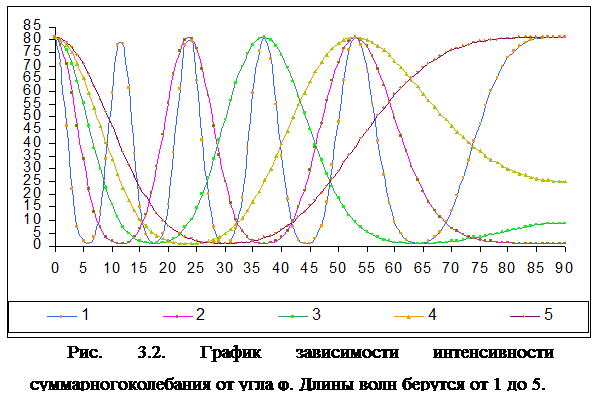
Рассмотрим график интенсивности суммарного колебания при разных параметрах. Угол θ изменяется в интервале [0; ] (это видно из рисунка 3.1), длина волны изменяется от 1 до 5.

2.3.2. Дифракция рентгеновских лучей

Дифракция рентгеновских лучей - процесс, возникающий при упругом рассеянии рентгеновского излучения и состоящий в появлении отклоненных (дифрагированных) лучей, распространяющихся под определенными углами к первичному пучку. Дифракция рентгеновских лучей обусловлена пространственной когерентностью вторичных волн, которые возникают при рассеянии первичного излучения на электронах, входящих в состав атомов. В некоторых направлениях, определяемых соотношением между длиной волны излучения и межатомными расстояниями в веществе, вторичные волны складываются, находясь в одинаковой фазе, в результате чего создается интенсивный дифракционный луч. Другими словами, под действием электромагнитного поля падающей волны заряженные частицы, имеющиеся в каждом атоме, становятся источниками вторичных (рассеянных) сферических волн. Отдельные вторичные волны интерферируют между собой, образуя как усиленные, так и ослабленные пучки излучения, распространяющиеся в разных направлениях.

 Скачать реферат