Рассеяние рентгеновских лучей на молекулах фуллерена

Как следствие, в степень инвариантности (4.2) основной вклад дает центральный максимум. Иначе говоря, высокая симметрия центрального максимума подавляет симметрийные особенности всех остальных характерных особенностей дифракционной картины.

Для детального исследования поворотной псевдосимметрии угловом распределении рассеянного рентгеновского излучения целесообразно вычислять функционалы сл

едующего вида:

(4.3)

Внешние интегралы по полярному углу имеют пределы, которые может задавать исследователь, что позволяет изучать поворотную псевдосимметрию в различных интервалах полярного угла. Иначе говоря, величины типа (4.3) дают количественные оценки поворотной псевдосимметрии дифракционной картины внутри кольца, заданного парой полярных углов q1 и q2. (см. рис.4.1).

Естественно разбить диапазон полярных углов [0, π/2] на поддиапазоны определенной ширины dq = q2 - q1 и провести вычисления коэффициентов псевдосимметрии для всех таких поддиапазонов.

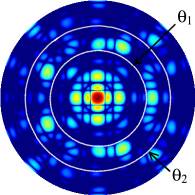
Рис.4.1. Кольцо на полярной диаграмме дифракционной картины, ограничивающее диапазон полярных углов [q1, q2].

Выше было указано, что при компьютерном моделировании углового распределения интенсивности рассеянных рентгеновских лучей функция I(q, Ф) представляется двумерным множеством числовых значений I(ql, jm) для конечных дискретных наборов углов ql = l Dq, l=1,…nq; Фm = m DФ, m =1,…nФ. Следовательно, при вычислении коэффициентов псевдосимметрии ha по результатам расчета углового распределения интенсивности рассеянных рентгеновских лучей двойные интегралы в выражении (4.2) превращаются в двойные суммы

Если нас интересует усредненная поворотная псевдосимметрия всей дифракционной картины, то степень инвариантности следующей формулой:

(4.4)

Если же мы хотим исследовать поворотную псевдосимметрию в различных поддиапазонах полярного угла (см. рис.4.1), то необходимо вычислять отношение сумм для соответствующих интервалов типа (4.3). Тогда коэффициенты псевдосимметрии представятся в виде:

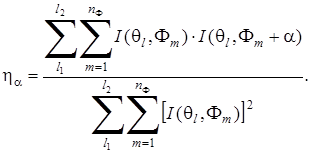(4.5)

где индексы l1 и l2 соответствуют значениям полярных углов q1 и q2

q1 = l1 Dq, q2 = l2 Dq. (4.6)

Задавая определенные значения угла поворота a можно вычислять коэффициенты псевдосимметрии ha дифракционных картин для поворотов различных порядков. Если нас интересует поворотная псевдосимметрия n-го порядка, то угол поворота a выражается соотношением.

an = 2p / n. (4.7)

Величину (4.7) далее будем называть углом поворота n-го порядка.

3.1.2. Компьютерное моделирование рассеяния рентгеновских лучей на молекулах и фрагментах кристаллических структур

В настоящей работе проводился расчет характеристик рентгеновского излучения, рассеянного конечным множеством атомов в условиях дифракции Фраунгофера. Первичное рентгеновское излучение представлялось плоской монохроматической волной с определенным волновым вектором k0 и длиной волны l.

Угловое распределение интенсивности рентгеновских лучей, рассеянных на конечном множестве атомов, представляется функцией I(q, Ф), зависящей от двух углов – полярного q и азимутального Ф. Углы q и Ф определяют направление на детектор рассеянных рентгеновских лучей, которое в условиях дифракции Фраунгофера совпадает с волновым вектором k рассеянной рентгеновской волны.

Полярный угол q отсчитывается от направления волнового вектора k0 первичной рентгеновской волны. Азимутальный угол Ф откладывается в плоскости, перпендикулярной вектору k0. Азимут Ф представляет собой угол между проекцией волнового вектора k рассеянной волны на эту плоскость и произвольно выбранной азимутальной оси.

Набор значений функции I(q, Ф) для всевозможных значений аргументов q и Ф часто называется дифракционной картиной.

В нашей задаче рассматривается рассеяние рентгеновских лучей в «переднюю» полусферу. Следовательно, полярный угол q принадлежит диапазону [0, π/2],. Азимутальный угол Ф принимает значения в интервале [0, 2π).

В качестве рассеивателей рассматривались молекулы и небольшие фрагменты кристаллов, т.е. трансляционно упорядоченных атомных структур. Месторасположение всех атомов задавалось с помощью декартовой системы координат, ось Z которой совмещалась по направлению с волновым вектором k0.

Так как задача решалась в рамках приближения дифракции Фраунгофера, то интенсивность рассеянного рентгеновского излучения представлялась формулой (3.37).

Алгоритм расчета углового распределения интенсивности рентгеновского излучения в условиях дифракции Фраунгофера был реализован в виде оригинальной компьютерной программы на алгоритмическом языке Object Pascal, разработанной в интегрированной среде Delphi-7.

Программа позволяет задавать значения химического номера атомов (для расчета функции атомного фактора), длины волны рентгеновских лучей.

Координаты центров атомов облучаемых объектов (т.е. рассеивателей) предварительно записывались во внешние файлы. В программе предусмотрена возможность выбора облучаемого объекта из заданного набора рассеивателей.

Так как в качестве рассеивающих объектов используются как молекулы, так и фрагменты кристаллов, то входными параметрами программы также являются кристаллохимические радиусы атомов и радиусы сферически симметричных молекул (кластеров).

Для расчета дифракционной картины диапазоны полярного q и азимутального Ф углов разбиты на интервалы Dq и DФ соответственно, количество которых задается пользователем. Для каждого интервала задано значение угла, согласно следующим формулам:

ql = l Dq,l=1,…nq, Фm = m DФ, m =1,…nФ,(4.8)

где nl и nm – количество интервалов разбиения полярного и азимутального углов соответственно.

Числа nl и nm связаны с длинами интервалов Dq и DФ следующими соотношениями:

nq = (π/2) / Dq и nФ = 2π / Dj(4.9)

Таким образом компьютерная программа позволяет рассчитать угловое распределение интенсивности рассеянных рентгеновских лучей в виде двумерного массива значений

Il,m = I(ql, jm). (4.10)

Величины Dq и DФ определяют дискретность расчета дифракционной картины.

Аргументы функции углового распределения интенсивности рентгеновского излучения (4.10), рассеянного исследуемым образцом, т.е. значения углов ql и jm (l = 1, …, nq; m =1,…nФ), представляют собой точки на полусфере.

Моделирующая программа визуализирует рассчитанное угловое распределение интенсивности рассеянного рентгеновского излучения Ii,j в виде двумерной (плоской) полярной диаграммы дифракционной картины. Полярный угол q откладывается по радиусу от центра картины, азимутальный угол Ф – по дуге окружности против часовой стрелки.

Величина интенсивности рассеянного излучения I(ql, jm) представляется различным цветом и оттенками. В данной программе используются пять основных цветов: коричневый, красный, желтый, бирюзовый и синий. Коричневый цвет отвечает максимальной интенсивности излучения, темно-синий – минимальной. Переход от одного основного цвета к следующему соответствует изменению интенсивности рассеянного излучения на порядок (т.е. в 10 раз).

 Скачать реферат