Рассеяние рентгеновских лучей на молекулах фуллерена

Характерно, что начальная деформация пружины в системе на рис.1.8. б не влияет на частоту колебаний.

2.1.3. Сложение колебаний

2.1.3.1. Сложение двух гармонических колебаний с одинаковыми амплитудами и частотами

Рассмотрим пример звуковых волн, когда два источника создают волны с одинаковой амплитудами A и частотами ω. На расстоянии от источников установим чувстви

тельную мембрану. Когда волна «пройдёт» расстояние от источника до мембраны, мембрана придёт в колебательное движение. Воздействие каждой из волн на мембрану можно описать следующими соотношениями, воспользовавшись колебательными функциями:

x1(t) = A cos(ωt + φ1),

(1.26)

x2(t) = A cos(ωt + φ2).

Для того, чтобы сосчитать колебание, с которым будет колебаться мембрана, просуммируем функции (1.26):

x(t) = x1 (t) + x2 (t) = A [cos (ωt + φ1) + cos (ωt + φ2)] (1.27)

Выражение, которое находится в скобках, можно записать иначе, воспользовавшись тригонометрической функцией суммы косинусов:

(1.28)

Для того чтобы упростить функцию (1.28), введём новые величины A0 и φ0, удовлетворяющие условию:

A0 = 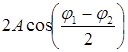φ0 = (1.29)

Подставим в функцию (1.28) выражения (1.29), получим

(1.30)

Таким образом, сумма гармонических колебаний с одинаковыми частотами ω есть гармоническое колебание той же частоты ω. При этом амплитуда суммарного колебания A0 и начальная фаза φ0 определяются соотношениями (1.29).

2.1.3.2. Сложение двух гармонических колебаний с одинаковой частотой, но разными амплитудой и начальной фазой

Теперь рассмотрим такую же ситуацию, изменив в функции (1.26) амплитуды колебаний. У функции x1 (t) заменим амплитуду A на A1, а у функции x2 (t) А на A2. Тогда функции (1.26) запишутся в следующем виде

x1 (t) = A1 cos(ωt + φ1), x2 (t) = A2 cos (ωt + φ2); (1.31)

Найдем сумму гармонических функций (1.31)

x= x1 (t) + x2 (t) = A1 cos(ωt + φ1) + A2 cos (ωt + φ2) (1.32)

Выражение (1.32) можно записать иначе, воспользовавшись тригонометрической функцией косинуса суммы:

x(t) = (A1cos(φ1) + A2cos(φ2)) cos(ωt) – (A1sin(φ1) + A2sin(φ2)) sin(ωt) (1.33)

Для того чтобы упростить функцию (1.33) введём новые величины A0 и φ0, удовлетворяющие условию:

(1.34)

Возведём каждое уравнение системы (1.34) в квадрат и сложим полученные уравнения. Тогда мы получим следующее соотношение для числа A0:

(1.35)

Рассмотрим выражение (1.35). Докажем, что величина под корнем не может быть отрицательной. Так как cos(φ1 – φ2) ≥ –1, значит, это единственная величина, которая может повлиять на знак числа под корнем (A12 > 0, A22 > 0 и 2A1A2 > 0 (из определения амплитуды)). Рассмотрим критический случай (косинус равен минус единице). Под корнем оказывается формула квадрата разности, что является величиной всегда положительной. Если мы начнём постепенно увеличивать косинус, то слагаемое, содержащее косинус тоже начнёт расти, тогда величина, стоящая под корнем не изменит свой знак.

Теперь рассчитаем соотношение для величины φ0, разделив второе уравнение системы (1.34) на первое и вычислив арктангенс:

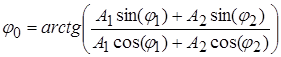(1.36)

А теперь подставим в функцию (1.33) значения из системы (1.34)

x = A0(cos(φ0) cosωt – sin(φ0) sinωt) (1.37)

Преобразуя выражение, стоящее в скобках по формуле косинуса суммы, мы получим:

x(t) = A0 cos(ωt + φ0) (1.38)

И опять получилось, что сумма двух гармонических функций вида (1.31) является также гармонической функцией того же вида. Точнее говоря, сложение двух гармонических колебаний с одинаковыми частотами ω представляет собой также гармоническое колебание с той же частотой ω. При этом амплитуда результирующего колебания определяется соотношением (1.35), а начальная фаза – соотношением (1.36).

2.2. Волны

2.2.1. Распространение колебаний в материальной среде

Рассмотрим колебания в материальной среде. Одним из примеров является колебание поплавка на поверхности воды. Если в роли наблюдателя выступит птица, пролетающая над поплавком, то она заметит, что поплавок образует вокруг себя окружности, которые, что удивительно, с течением времени, удаляясь, увеличивает радиус. Но если в роли наблюдателя будет человек, стоящий на берегу, то он увидит «горбы» и «впадины», которые, чередуясь, приближаются к берегу. Это явление называют бегущей волной.

Рис. 2.1. Схематичное изображение поперечной волны.

Мы видим, что причиной движения является шарик №1, т.е. поплавок. Он с помощью взаимодействия вовлекает в движение шарик №2, шарик №2 вовлекает №3 шарик, и т.д. Но взаимодействие между частицами происходит не мгновенно, поэтому шарик №2 будет отставать по времени. Также можно заметить, что шарик №13 колеблется так же, как и №1. Тогда можно сделать вывод, что шарик №2 будет отставать от №1 на 1/12 периода.

Отсюда периодом волны(T) можно назвать период колебаний шарика №1, амплитудой волны(A) – максимальное отклонение шарика от горизонтальной оси, а длиной волны (λ) – минимальное расстояние между максимумами ближайших горбов или минимумами ближайших впадин.

В ранее рассмотренном примере волна распространялась перпендикулярно колебаниям источника, иначе говоря, была рассмотрена поперечная волна.

Продольные волны – волны, распространяющиеся параллельно движению источника. Если рассматривать продольные волны схематически (рис.2.2), то можно заметить, что с течением времени источник колебаний (шар №1) колеблется влево-вправо и вовлекает в такое же колебательное движение остальные частички. Тогда, для продольной волны, определение периода волны, описанное выше, останется неизменным, а определения длины волны и амплитуды будут выглядеть иначе. Обобщенные понятия будут выглядеть так: длина волны – минимальное расстояние между шариками, двигающихся с одинаковыми фазами; амплитуда волны – максимальное отклонение от положения равновесия.

 Скачать реферат