Рассеяние рентгеновских лучей на молекулах фуллерена

Содержание

Цели работы 4

2. Теоретическая часть. 5

2.1. Колебания. 5

2.1.1. Одномерные колебательные движения. 5

2.1.2. гармонические колебания. 7

2.1.3. Сложение колебаний. 15

2.1.3.1. Сложение двух гармонических колебаний с одинаковыми амплитудами и частотами. 15

2.2. Волны 17

2.2.1. Распространение колебаний в материальной среде. 17

2.2.2. Вол

новая функция. 20

2.2.3. Электромагнитные волны 24

2.2.4. Рентгеновские лучи. 26

2.3. Дифракция волн. 29

2.3.1. Дифракция и интерференция волн. 29

2.3.2. Дифракция рентгеновских лучей. 33

2.3.3. Интерференционная картина от n источников расположенных на одной прямой 35

2.3.4. Атомный фактор. 36

3.5. Дифракция Фраунгофера рентгеновских лучей на атомах кристалла 38

3. Практическая часть. 50

3.1. Псевдосимметрия. 50

3.1.1. Поворотная псевдосимметрия дифракционных картин. 50

3.1.2. Компьютерное моделирование рассеяния рентгеновских лучей на молекулах и фрагментах кристаллических структур. 55

3.1.3. Псевдосимметрия дифракционных картин рассеяния рентгеновских лучей на фрагментах кристаллов фулеритов. 61

4. Выводы 70

5. Список используемой литературы 71

6. Приложения. 72

6.1. Приложение 1. Комплексные числа. 72

6.1.1. Определение комплексного числа. 72

6.1.2. Геометрическая интерпретация комплексных чисел. 73

6.1.3. Сопряженные комплексные числа. 75

6.1.5. Экспоненциальная форма комплексных чисел. 75

6.2. Приложение 2. Определение координат вершин шестидесятигранника 76

Цели работы

1. Компьютерное моделирование рассеяния рентгеновских лучей на молекулах фуллерена и фрагментах кристаллов фуллеритов.

2. Исследование поворотной псевдосимметрии углового распределения интенсивности рассеянных рентгеновских лучей.

2. Теоретическая часть

2.1. Колебания

2.1.1. Одномерные колебательные движения

Рассмотрим одномерное периодическое движение материальной точки. Периодичность движения означает, что координата точки x является периодической функцией времени t:

x = f(t). (1.1)

Иначе говоря, для любого момента времени выполняется равенство

f(t + T) = f(t), (1.2)

где постоянная величина Т называется периодом колебания.

Существенно, что координата может быть не только декартовой, но и углом и т.д.

Существует множество разновидностей периодического движения. Например, таковым является равномерное движение материальной точки по окружности.

Рис.1.1. Шарик, подвешенный на пружине.

Характерные примеры физических систем, совершающих колебательные движения, приведены на рисунках 1.1. – 1.6. Следует заметить, что в примерах на рис.1.1, 1.2. и 1.4. тела совершают колебания вдоль прямых линий. В примере 1.5. одномерные колебания совершает поверхность жидкости в трубке (или маленькая частица, плавающая на

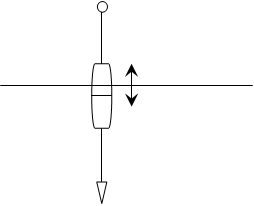Рис.1.3. Шарик, подвешенный на нити.

Рис.1.4. Поплавок на поверхности жидкости.

Рис.1.5. U-образная трубка с жидкостью.

Рис.1.6. Электрический контур, содержащий конденсатор с емкостью C и катушку с индуктивностью L.

В примере 1.3. периодически меняется угол отклонения. Наконец, в примере 1.6. периодически изменяется заряд конденсатора и сила тока в катушке. Тем не менее, все эти физические процессы описываются одинаковыми математическими функциями.

2.1.2. гармонические колебания

Наиболее простой разновидностью колебаний являются гармонические. Координата материальной точки с течением времени при гармонических колебаниях изменяется по закону

x(t) =A cos(wt + j0) (1.3)

где A – амплитуда смещения (максимальное смещение точки от положения равновесия), w – частота, связанная с периодом соотношением

w = 2p / T. (1.4)

Положением равновесия называется месторасположение материальной точки, в котором сумма действующих на нее сил равна нулю.

Аргумент косинуса wt + j0 в функции (1.3) называется фазой колебания. Видно, что фаза является безразмерной величиной и линейной функцией времени. Постоянная величина j0 называется начальной фазой.

Колебания физических систем, приведенных на рис.1.1. – 1.6. совершали бы строго гармонические колебания при следующих дополнительных условиях:

Система 1.1. – при отсутствии сопротивления воздуха, система 1.2. – при отсутствии терния, система 1.3. – при малых углах и отсутствии сопротивления воздуха, системы 1.4. и 1.5. – при отсутствии вязкости жидкости, система 1.6. – при отсутствии активного сопротивления катушки и проводов.

Рассмотрим для простоты сначала одномерные гармонические колебания, когда материальная точка смещается вдоль одной прямой.

Вычислив производную функции (1.3) по времени получим скорость материальной точки:

v(t) = - w A sin(wt+j0) (1.5)

Видно, что скорость является также периодической функцией времени.

Теперь возьмем производную от функции (1.5) по времени и получим ускорение материальной точки.

a(t) = - w2 A cos(wt+j0) (1.6)

Сравнивая функции (1.3) и (1.6) получим что координата и ускорение связанны следующим выражением

a(t) = - w2 x(t),(1.7)

которое выполняется в любой момент времени.

Иначе говоря, при любых одномерных гармонических колебаниях ускорение частицы прямо пропорционально её координате, причем коэффициент пропорциональности отрицательный.

Рис.1.7. Зависимости от времени координаты (кружочки), скорости (квадратики) и ускорения (треугольники) частицы, совершающей одномерные гармонические колебания. Амплитуды А=2, период Т=5, начальная фаза j0=0.

 Скачать реферат