Рекурсия
fla1(2×s)=2×fla1(s) - 1 (s³1). (16)
Аналогичные рассуждения показывают, что
fla1(2×s+1)=2×fla1(s) + 1 (s³1). (17)
Величины fla1(n) назовем числами Флавия. Соотношения (16) и (17) сразу же позволяют написать следующую рекурсивную программу-функцию вычисления значений fla1(n).
fla1(2s + q)=2×q+1 (s³0, 0£q<2×s) (18)
Отсюда получаем еще один рекурсивный алгоритм для вычисления чисел Флавия (см. ниже). При этом вспомогательная рекурсивная функция power(n,0) вычисляет значение s, удовлетворяющее соотношению (18), то есть уменьшенное на 1 количество цифр двоичного разложения n, а функция fla2(n) непосредственно вычисляет число Флавия для заданного n.
A3. Еще один способ нахождения чисел Флавия дается программой-функцией flavec(v), где v=(1 2 3 . n)T - вектор. Подавать такой вектор в качестве аргумента необязательно. Проще обращаться к flavec(v) c помощью функции fla3(n), где по заданному n генерируется соответствующий вектор v. Отметим, что в flavec(v) используется рекурсивный алгоритм непосредственного вычеркивания каждого второго числа. При этом вектор v перестраивается при каждом новом перемещении по кругу.
Контрольные примеры.
1. fla1(6)=5fla2(6)=5fla3(6)=5
2. fla1(11)=7 fla2(11)=7 fla3(11)=7
3. fla1(1000)=997fla2(1000)=997fla3(1000)=997
B. Решение первой задачи Флавия в общем случае.
Ниже рассмотрены два варианта B1-B2 решения задачи 1 в общем случае. Первый из них представляет прямое обобщение алгоритма из пункта A3 и реализует рекурсию по каждому вычеркнутому элементу. Во втором варианте рекурсия организована по отдельным проходам по окружности.
B1. Способ A3 решения задачи 1 при k=2 хоть и несколько громоздкий, но он достаточно просто переносится на общий случай. При этом естественно считать k аргументом функции.Тогда решение задачи дает рекурсивная программа-функция flave(v,k), где v=(1 2 3 . n)T - вектор. Однако проще использовать для этих целей функцию fla4(n,k), формирующую по заданному целому n требуемый вектор v, а затем уже обращающуюся k flave(v,k).
B2. Приведенный ниже способ решения первой задачи Флавия отличается от предыдущего лишь способом организации рекурсии. Здесь она реализована не по каждому вычеркнутому элементу, а по отдельным проходам по окружности. Решение задачи дается программой-функцией flavmek(v,k), где v=(1 2 3 . n)T - вектор. Однако проще использовать для этих целей функцию fla5(n,k), формирующую по заданному целому n требуемый вектор v, а затем уже обращающуюся к flavmek(v,k). Обратите внимание на используемый в fla5(n,k) метод формирования вектора v.
Контрольные примеры.
1. fla4(6,2)=5 fla5(6)=5
2. fla4(41,3)T =[16 31] fla5(11) T =[16 31]
3. fla4(1000,5)T=[563 763 802 73] fla5(1000) T=[563 763 802 73]
С. Решение второй задачи Флавия в общем случае.
Пусть функция flav(v,k), где v=(1 2 . n)T решает поставленную задачу и пусть w - вектор, полученный из v вычеркиванием одного k-го компонента. После каждой такой операции будем организовывать рекурсивный вызов flav(w,k), прекращая вычисления тогда, когда длина вектора станет равной единице. Пусть le - длина вектора v и s=mod(k,le). Нетрудно видеть, что после одного вычеркивания получим:
w=(1 2 . le-1)T при s=0 ,
w=(2 3 . le)T при s=1 ,
w=(s+1,s+2, .,le,1,2, .,s-1) при s>=2 .
Поэтому функцию flav(v,k) и обращающуюся к ней функцию fla6(n,k) можно определить следующим образом:
Контрольные примеры.
fla6(10,5)=3 fla6(5,10)=4 fla6(1000,7)=404 .
13.4 Системы счисления
A. Перевод чисел из десятичной системы в p-ичную систему
Не ограничивая общности речь можно вести о неотрицательных числах.Пусть pÎ{2,3,…} и цифры p-ичной системы - это последовательные десятичные числа: 0, 1, . p-1. Рассмотрим 6 конкретных задач. В трех первых из них речь идет о переводе естественным образом заданных десятичных чисел в p-ичную систему счисления. В следующих трех задачах речь идет о переводе десятичных чисел, цифры которых заданы в виде последовательных компонентов векторов, в p-ичную систему счисления. Во всех случаях результат формируется в виде вектора, компоненты которого p-ичные цифры исходного числа.
Задача 1. Составить программу-функцию перевода целых неотрицательных десятичных чисел m в систему счисления по основанию p.
Решение. Функция dec_p_i(m,p) решает поставленную задачу, используя рекурсивный алгоритм последовательного деления. Результат формируется в виде вектора, компоненты которого p-ичные цифры m.
Контрольные примеры.
Замечания.
1. Если разряды p-ичного числа необходимо формировать не от старшего разряда, а от младшего и далее, то в программе dec_p_i() первый и второй аргументы функции stack() необходимо поменять местами.
2. При переводе неотрицательных десятичных чисел в конкретную систему счисления, в функции dec_p_i() достаточно иметь один аргумент. Например, перевод в двоичную систему можно осуществлять следующей программой-функцией dec_b_i(m).
Контрольные примеры.
Как мы уже отмечали при реализации функций dec_p_i(m,p) и dec_b_i(m) использован рекурсивный вариант алгоритма последовательного деления - выделения цифр p-ичной системы для целых чисел. Пояснений требуют лишь фрагменты вида identity(1)×x. Дело в том, что функция stack() в качестве своих аргументов использует векторы или матрицы. И смысл записи identity(1)×x состоит в превращении скаляра х в матрицу размера 1´1 с элементом x.
Задача 2. Составить программу-функцию перевода правильной неотрицательной десятичной дроби y в систему счисления по основанию p.
Решение. Функция dec_p_f(y,p,k) решает поставленную задачу, используя рекурсивный алгоритм последовательного умножения. Результат формируется в виде вектора с не более чем k (k=1,2,…) компонентами, которые суть p-ичные цифры числа y, начиная от старших разрядов и далее.

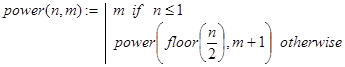
![]()
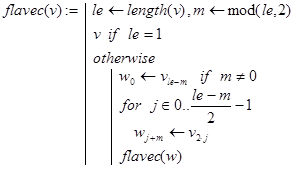
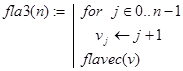
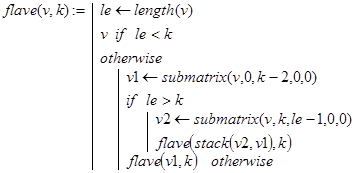
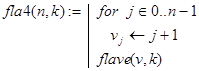

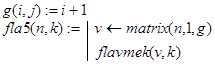
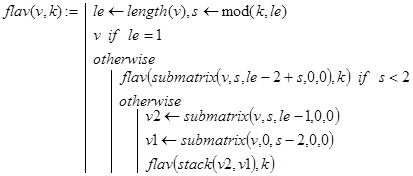
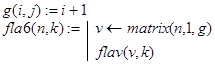
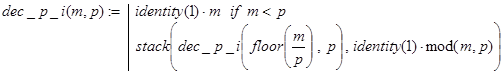
![]()
![]() .
.

![]()
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
