Рекурсия

Контрольные примеры.

Далее, если n ³2 и dn(n)=2, то число n – простое. Однако проверка n на простоту этим способом весьма неэкономна.

3.18 Простые числа

Зада

ча 22. Составить программу-функцию проверяющую, является ли заданное натурально число n простым?

Решение. Пусть рекурсивная функция isprim(n) является решением задачи и

Дальнейшие рассуждения являются иллюстрацией использования классического приема “вложения” (Дж. Маккарти, 1962). Перейдем к рассмотрению следующей обобщенной задачи. Пусть a, b, n- натуральные числа и 2£a£b£n. Верно ли, что заданное n не делится ни на одно целое из отрезка [a, b]? Пусть эту задачу решает функция

Ниже приведено три рекурсивных варианта реализации этой функции. По первому из них проверке на делитель n последовательно подвергаются числа: a, a+1, … , b; по второму - эти же числа в обратном порядке и, наконец, по третьему - a, b, a+1, b-1, … .

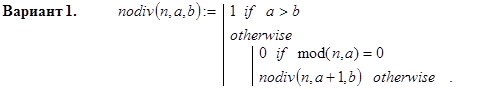
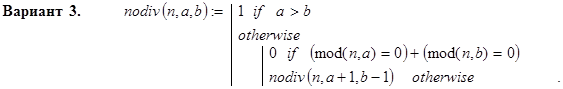
Контрольные примеры.

Далее, натуральное число n³2 является простым, если оно не имеет делителей на отрезке , поэтому характеристическая функция isprim(n) через функцию nodiv(n,a,b) может быть выражена так:

Контрольные примеры.

Задача 23. Составить программу-функциюpi(x), которая подсчитывает количество простых чисел, не превосходящих заданное число x.

Решение. С помощью функций nodiv() или isprim() рекурсивный вариант функции pi(x) строится достаточно просто, исходя из такого декомпозиционного утверждения. Количество простых чисел, не превосходящих x, составляется из количества простых чисел меньших или равных x-1 плюс значение функции isprim(x). Поэтому:

Контрольные примеры.

Задача 24. Составить программу pn(n), которая вычисляет n-ое простое число (n – натуральное).

Решение. Предварительно напишем рекурсивную подпрограмму-функ-цию minp(m) нахождения наименьшего простого числа, большего или равного m (m – натуральное число). Сделать это можно, например, так:

Контрольные примеры.

Тогда искомая функция pn(n) может быть определена так:

Контрольные примеры.

3.19 Схема Горнера

Задача 25. Составить программу-функцию вычисления значений многочлена по схеме Горнера.

Решение. Пусть f(x) многочлен с вещественными или комплексными коэффициентами и v – вектор этих коэффициентов:

(8)

(9)

Вычисление f(x) в точке x по схеме Горнера проводится от самых внутренних скобок и далее в соответствии с представлением:

Отсюда ясно, как записать рекурсивный и не рекурсивный варианты алгоритмов вычисления f(x). Нас интересует только первый из них. Параметрами задачи можно считать вектор v и точку a для вычисления f(a). Тривиальный случай – многочлен нулевой степени: f(a) = a0. Декомпозиция получается из указанной выше расстановки скобок в записи f(x). Соответствующая программа-функция выглядит, например, так.

Контрольные примеры.

Замечание. Параметр n – это константа, равная степени многочлена. По вектору v она определяется однозначно. Однако в каждом рекурсивном вызове проводится перевычисление n. Избежать лишней вычислительной работы в подобных ситуациях можно двумя способами. Или определять такие константы заранее вне текста программы-функции или передавать их значения через дополнительные аргументы функции.

3.20 Деление многочлена на двучлен

Задача 26. Составить программу-функцию, по которой для многочлена (8) с коэффициентами, составляющими вектор (9) и двучлена x-x0 (x0 - вещественное или комплексное число), вычисляется вектор c:

такой, что

и

Решение. Если в соотношении, связывающем многочлены f(x) и q(x), осуществить приведение к общему знаменателю и приравнивание коэффициентов при одинаковых степенях x, то для определения компонент вектора c получим следующую систему линейных уравнений.

Отсюда вытекает, что c = qu(v,x0), где рекурсивное определение функции qu() может выглядеть, например, так.

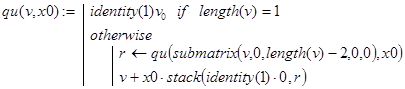
Контрольный пример.

Иными словами:

3.21 Произведение двух многочленов

Задача 27. Пусть коэффициенты многочленов fn(x) и gm(x) заданы компонентами векторов v и w:

(10)

(11)

Составить рекурсивную программу-функцию вычисляющую коэффициенты многочлена hn+m(x)=fn(x)×gm(x) и возвращающую их в виде компонентов вектора:

Решение. Поскольку

где

 Скачать реферат