Рекурсия

Для отыскания решения многих задач часто используется метод дихотомии, называемый также методом последовательного деления пополам, бисекции или вилки. В некоторых ранее рассмотренных задачах мы уже сталкивались с этим методом. В нашем случае, когда ищется корень уравнения, суть его в следующем. Пусть e > 0 задано. Делим отрезок [a, b] точкой с=(b+a)/2 на две равные части и в качестве нового

отрезка [a, b] берем ту из его половин, для которой снова f(a)×f(b) £ 0 и т.д. Ясно, что на некотором шаге будем иметь отрезок [a, b] такой, что b – a < 2×e и f(a)×f(b) £ 0. Следовательно, приближенное решение найдено и оно равно (b + a)/2.

А как записать предложенный алгоритм с использованием рекурсии? Оказывается все достаточно просто.

Контрольные примеры.

1. y(x):= x3dicho(y, -1, 1, 0.01) = -0.008

2. f(u)=u×(u + sin(u) – 3)×exp(cos(u))

dicho(f, 1, 3, 0.0001) = 2.18f(2.18)=0

Задача 16. Пусть функция f(x) вещественной переменной x непрерывна на отрезке [a, b]. Составить программу нахождения на [a, b] любого вещественного корня f(x). При отсутствии корней, должно быть выдано значение ¥ (10307).

Решение. Отличие постановки этой задачи от предыдущей в том, что здесь априори ничего неизвестно о знаках функции на концах отрезка и, следовательно, корней f(x) уже может и не быть. Однако метод дихотомии с успехом может быть применен и в данном случае. Соответствующий алгоритм может быть записан так.

Контрольные примеры.

Рассмотрим функции примеров из предыдущей задачи. Имеем:

dichot(y,1,7,0.001)=10307 , dichot(f,2.17,3,0.0001)=2.18 .

Периодическое продолжение

Задача 17. Составить программу, которая для функции g(x), определенной при x Î [a,b), строит функцию peri(g,a,b,x), являющуюся периодическим продолжением g(x) на всю действительную ось c периодом w = b – a.

Решение. Нам, очевидно, требуется определить функцию следующего вида.

На языке Mathcad это будет выглядеть практически так же:

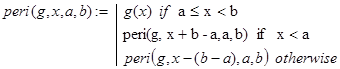
Заметим, что при x находящемся вдали от промежутка [a,b) вычисления значения функции peri() требует значительного количества рекурсивных вызовов. Происходит это по той причине, что за один такой вызов мы продвигаемся в направлении [a,b) лишь на расстояние w=b-a.

Значительно эффективней проводятся вычисления по функции F(g,x,a,b) также являющейся периодическим продолжением g(x) на всю числовую ось.

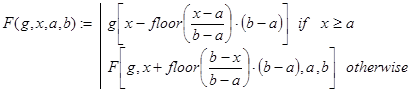
Контрольные примеры.

1. Пусть y(x) = x2×sin(x). Тогда:

peri(y,1,0,2) = 0.841 peri(y,3,0,2) = 0.841

peri(y,-1,0,2) = 0.841 peri(y,1001,0,2)=0.841

2. На рис. 3.4 изображен график функции H(t), являющейся периодическим продолжением функции y(x)= x2×sin(x) для x Î [-10, 0). H(t) построено с помощью программы-функции F(), а график выведен на промежутке [-10,20) с шагом h=0.1.

t:= -10,-9.9 20 H(t):=perri(y,t,-10,0)

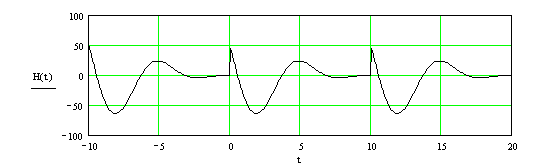
Рис. 3.4 Периодическое продолжение функции y(x)= x2×sin(x)

для x Î [-10, 0).

3.14 Функция Аккермана

Задача 18. Пусть n и m целые неотрицательные числа. Написать программу, вычисляющую классическую в теории рекурсии функцию Аккермана:

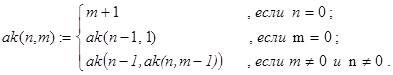(5)

Решение. Вычислить функцию Аккермана, исходя непосредственно из определения (5), удается лишь для некоторых малых n и m. Связано это со сложностью и необычностью рекурсивного определения. В общем случае не только ak() вычисляется через ak(), но и второй из аргументов функции также требует рекурсивного вызова ak(). Соответствующая программа-функция может быть записана так:

Контрольные примеры.

Следующий вариант программы для вычисления функции Аккермана включает в себя лишь один рекурсивный вызов:

Замечание. Для m=0 4 справедливы соотношения [5, с. 69]:

Эти формулы могут оказаться полезными при построении контрольных примеров для отладки новых более эффективных вариантов программ вычисления функции Аккермана.

В работе [5, c. 256-260] приведен нерекурсивный вариант алгоритма вычисления значений функции Аккермана.

3.15 Функция Маккарти

Задача 19. Функция Маккарти. Показать, что для приведенной ниже рекурсивной программы-функции

при целочисленных значениях n справедлива формула:

(6)

Решение. Относительно параметра n возможны три случая:

n > 100,90£ n £100, -¥ < n<90.

В первом из них в силу базы рекурсии следует, что makkarti(n)=n-10. Во втором случае:

Наконец, всякое начальное n<90 в соответствии с декомпозицией через конечное число рекурсивных вызовов приводит ко второму случаю. Отсюда опять makkarti(n)=91. Таким образом (6) справедливо во всех случаях.

Заметим, что из проведенных рассуждений вытекает, что рассматриваемая функция может быть определена более просто, например, так:

3.16 Функция Кадью

Задача 20. Показать, что для приведенной ниже рекурсивной программы-функции

при целочисленных значениях x справедлива формула:

(7)

Решение. При y=0 и z=1 имеем z=y!. Далее из характера декомпозиции функции cadiou() ясно, что z=y! остается инвариантом в ходе рекурсивных вызовов. Вместе с условием завершения x=y это и дает z=x! и (7) установлено.

3.17 Количество делителей

Задача 21. Количество делителей. Составить программу-функцию подсчета для натурального числа n количества всех его делителей.

Решение. Перейдем к более общей задаче. Подсчитаем для натурального числа n количества всех его делителей, меньших или равных заданному натуральному числу x. Пусть dn(n) и dnx(n,x) - соответственно функции для решения исходной и обобщенной задач. Очевидно, что dn(n)=dnx(n,n).

Рекурсивную функцию dnx(n,x), по которой последовательно подвергаются испытанию на делители n все числа от 1 до x включительно, можно определить так:

 Скачать реферат