Рекурсия

Далее, декомпозиция определяется таким утверждением. Если уже построена матрица ma точек для 2×(n-1) вложенных квадратов, то, пополнив её точками матрицы , получим матрицу точек для 2×n таких квадратов. Соответствующая рекурсивная функция, базирующаяся на этих фактах, может выглядеть так:

src="images/referats/14053/image163.png">

Контрольный пример. Результат вычислений представлен на рис. 3.5 c неодинаковым масштабом по осям.

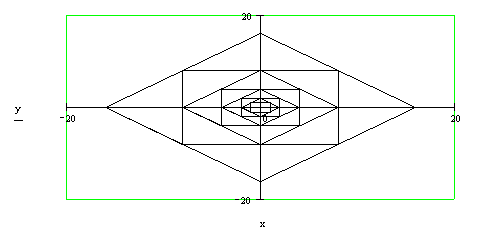
Рис. 3.5. Вложенные 2×n квадратов (n=4)

Задача 35. Вложенные многоугольники. Пусть на плоскости задан правильный n-угольник, вписанный в единичную окружность одна из вершин которого имеет координаты (cos(a), sin(a)), где a - некоторый угол. Второй правильный n-угольник строится так, что его вершины являются серединами сторон первого многоугольника и т.д. Составить рекурсивную программу-функцию, которая по заданному натуральному n строит систему из n вложенных друг в друга описанным образом многоугольников, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис. 3.6).

Решение. Это задача в каком-то смысле является обобщением предыдущей. Здесь выводятся правильные вписанные n-угольники, количество их не обязательно четно и первая из вершин начального n-угольника может лежать в любой точке единичной окружности. Правда, здесь многоугольники не “описываются” один вокруг другого, а “вписываются” друг в друга. Но существа дела это не меняет.

Прежде всего, составим программу, которая формирует массив вершин правильного n-угольника, вписанного в окружность радиуса r и содержащего вершину (r×cos(a) r×sin(a)). Сделать это можно, например, так:

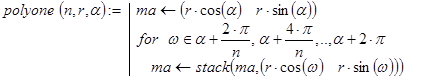
Тогда массив polyone(n,1,a) может служить базой рекурсии. Более того, эта функция при правильном выборе r и a позволяет получить массив вершин любого из следующих вписанных n-угольников, что помогает организовать и декомпозицию. Если уже построена матрица ma точек для (n-1)-го вписанного правильного n-угольника, то, пополнив её точками матрицы:

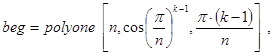
получим матрицу точек для 2×n таких многоугольников. Соответствующая рекурсивная функция, реализующая эти идеи, может выглядеть так:

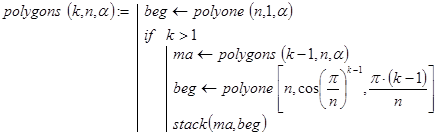
Контрольный пример. Результат вычислений представлен на рис. 3.6 c неодинаковым масштабом по осям.

Рис. 3.6. k вложенных правильных n-угольников (k=20, n=6)

Несколько слов перед формулировкой новой задачи. В основах анализа [8, с. 17-38] операции сложения и умножения над натуральными числами определяются рекурсивным способом, опираясь на аксиомы Пеано “о существовании последующего числа” и “индукции”. Первая из названных аксиом звучит так: “для каждого натурального x имеется и притом только одно натуральное число, называемое его последующим и обозначаемое число x¢ ”. Постараемся промоделировать указанные выше и некоторые иные операции.

Моделирование арифметических операций

Задача 36. Для целых неотрицательных чисел n, m разрешены операции:

нахождения последующего числа (n+1) и предыдущего числа n-1 (n>0). Промоделировать с помощью рекурсивных функций операции нахождения суммы (n+m), разности (n-m (n³m)), умножения (n×m), возведения в степень nm (n>0), частного и остатка при делении n на m (n/m).

Решение.

A. Сумма: a+b. Очевидноесоотношение

задает одновременно и базу рекурсии и правило декомпозиции. По нему и построена следующая рекурсивная программа-функция:

Контрольный пример:

B. Разность: a-b (a³b). В данном случае база рекурсии и декомпозиция могут быть извлечены из соотношения:

Соответствующая рекурсивная программа-функция выглядит так.

Контрольный пример:

C. Умножение: a×b. Будем считать, что операция сложения уже определена. Тогда соотношение, из которого легко извлекаются база и декомпозиция для данного случая выглядит следующим образом:

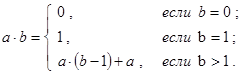
Соответствующая рекурсивная программа-функция может быть записана, например, так:

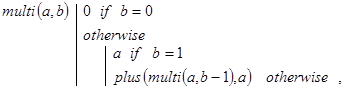
Контрольный пример:

D. Возведение в степень: ab (a¹0). Будем считать, что операция умножения уже определена. Тогда:

и рекурсивная программа-функция возведения в степень может быть задана так:

Контрольный пример:

E. Частное и остаток: a/b (b>0). В данной задаче речь идет об отыскании величин q и r из представления: a=q×b+r (0£r<b, q³0). Будем предполагать, что операция вычитания уже определена, а ответ должен быть возвращен в виде вектора с двумя компонентами: (q r)T. Если a<b, то q=0 и r=a. Этот факт и определяет базу рекурсии. Если же b>a, то a/b=1+(a-b)/b, что позволяет организовать декомпозицию. Все сказанное учтено в рекурсивной функции divi(q,a,b). В ней первый аргумент q является вспомогательным параметром. При обращениях к divi() он должен определять базовое значение частного, то есть быть равен нулю. Однако проще решать задачу с помощью вспомогательной функции div(a,b), возлагая на неё решение вопроса о правильном значении вспомогательного параметра вызовах divi(). Это довольно типичный случай при обобщениях исходной задачи за счет введения дополнительных параметров.

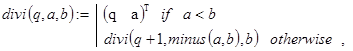
Контрольный пример.

 Скачать реферат