Рекурсия

то вполне можно организовать рекурсию по параметру m - степени второго сомножителя. И в качестве решения может быть предложена следующая функция:

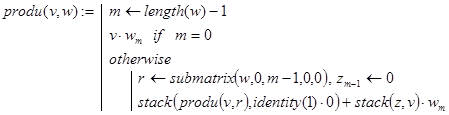
Ясно, что аналогично можно было бы реализовать рекурсию и по параметру n - степени первого сомножителя. В любом случае величины m и n определяют количество рекурсивных обращен

ий. Поэтому в данной задаче рекурсию выгодно реализовывать по параметру со значением, равным min(n,m).

Контрольный пример.

3.22 Произведение биномов

Задача 28. Составить программу-функцию возвращающую коэффициенты многочлена g(x), который получается в результате перемножения биномов (x-vk): (k=0,1,…n-1; n³1):

Решение. Будем считать, что свободные члены биномов заданы в виде компонентов некоторого вектора v: а результат вычислений должен возвращаться также в виде вектора. Поскольку

то несложно организовать рекурсию по количеству перемножаемых биномов. Соответствующая программа функция могла бы выглядеть так:

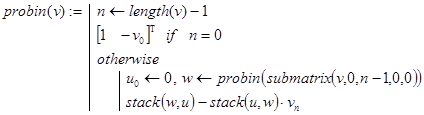
Контрольный пример.

3.23 Деление многочлена на многочлен

Задача 29. Пусть выполнены соотношения (10)-(11), то есть многочлены fn(x) и gm(x) степеней n и m (n,m³0) соответственно заданы своими коэффициентами в виде компонентов векторов v и w. Пусть, далее, при m=0, то есть если gm(x) есть константа, gm(x)¹0. Составить программу-функцию нахождения частного q(x) и остатка r(x) при делении fn(x) на gm(x):

fn(x)=q(x)×gm(x)+r(x), (12)

где степень r(x) меньше m (при m=0 r(x)º0).

Решение. Представление (12) единственно. В дальнейшем нам удобно считать, что степень r(x) равна m-1 с возможно нулевыми коэффициентами при старших степенях x.

При m=0 решение задачи очевидно:

q(x)=fn(x)/w0,r(x)=0. (13)

Далее, при n<=m имеем

(14)

Пусть n>m и q1(x) и r1(x) - частное и остаток от деления (fn(x)-an-1)/x на gm(x):

Из этого соотношения вытекает, что

Вместе с (12) это дает:

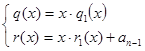(15)

Если соотношения (13)-(14) рассматривать в качестве базы рекурсии, то равенства (15) определяют декомпозицию. Считаем, что в результате вычислений должен быть сформирован и возвращен составной вектор qr=[q r]T, где q и r соответственно векторы коэффициентов многочленов q(x) и r(x). Соответствующая программа-функция, реализующая эти идеи, выглядит так:

Контрольные примеры.

Замечание. Функция poldiv() возвращает составной вектор [q r]T , в котором второй компонент-вектор r может содержать “ведущие” нули. При необходимости эти нули можно погасить, то есть выделить из r подвектор, начинающийся с первого из ненулевых компонент r. Сделать это можно, например, с помощью приведенной ниже рекурсивной функции nulera(u). Если все компоненты u равны нулю, то nulera(u) возвращает 0.

3.24 Разбиение целого на части

Задача 30. Составить программу-функцию подсчета количества x(m) разбиений натурального числа m, то есть его представления в виде суммы натуральных чисел.

Решение. Пусть, например, m=6. Тогда разбиениями m являются его представления в виде:

6;

5+1;

4+2, 4+1+1;

3+3, 3+2+1, 3+1+1+1;

2+2+2, 2+2+1+1, 2+1+1+1+1;

1+1+1+1+1+1;

Таким образом, x(m)=11 и понятно, что простым перебором возможных случаев уже при m>10 справиться с задачей достаточно сложно.

Для решения исходной задачи перейдем к рассмотрению обобщенной задачи. Составить программу-функцию подсчета количества P(m,n) разбиений натурального числа m со слагаемыми, не превосходящими n.Ясно, что x(m)=P(m,m). Поэтому, достаточно научиться вычислять значения функции P(m,n). Но для неё нетрудно выделить рекурсивную базу и указать правило декомпозиции. Сделать это можно исходя из следующих вполне прозрачных свойств этой функции.

1. P(m,1)=1 - существует только одно разбиение m, в котором слагаемые не превосходят единицы, а именно: m=1+1+…+1.

2. P(1,n)=1 - число единица имеет только одно представление при любом n.

3. P(m,n)=P(m,m) при n>m - слагаемые, большие m в разбиениях отсутствуют.

4. P(m,m)=P(m,m-1)+1 - существует лишь одно разбиение со слагаемым равным m. Все иные разбиения имеют слагаемые не превосходящие m-1.

5. P(m,n)=P(m,n-1)+P(m-n,n) (n<m). Обоснование этого соотношения проводится так. Все разбиения m на сумму слагаемых, не превосходящих n можно разбить на два непересекающихся класса: суммы, не содержащие n в качестве слагаемого и суммы, содержащие такое n. Количество элементов первого класса равно P(m,n-1), а количество элементов второго класса подсчитаем так. Без учета слагаемого n суммы элементов второго класса равны m-n. Значит их общее количество равно P(m-n,n) и, следовательно, общее количество элементов второго класса также равно этой величине. Тем самым свойство 5 установлено.

Первые два свойства определяют базу рекурсии, а три следующие задают декомпозицию. Строго в соответствии с этими утверждениями и составлена рекурсивная программа-функция deco(n,m) для вычисления величины P(m,n).

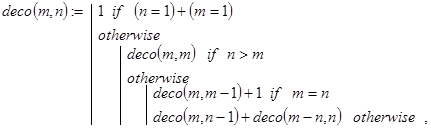
Контрольные примеры.

3.25 Максимальный и минимальный элементы

Пусть одномерный массив задан вектором Часто возникает задача поиска максимального (минимального) элемента v. Вне зависимости от того, идет ли речь о нахождении максимального по значению элемента или его позиции в v, поиск можно реализовать за один просмотр массива. Правда в последнем случае решение может оказаться неоднозначными и постановка задачи требует уточнения. Например, отыскивается позиция максимального элемента с наименьшим индексом. В любом случае сравнение характеристик различных алгоритмов поиска проводят по количеству тех или иных выполняемых ими операций. Чаще всего это операции сравнения.

 Скачать реферат