Рекурсия

Контрольные примеры.

Понять процесс реализации рекурсивных вызовов, то есть декомпозицию, и возвратов управления при организации отложенных вычислений facto(n) можно из схемы рис. 3.1 (n = 3). Там около стрелок в круглых скобках жирными цифрами указан

ы номера последовательных шагов вычислений: (1), (2), (3) - декомпозиция; (4), (5), (6) - отложенные вычисления.

Рис. 3.1. Схематическое изображение рекурсивных вызовов и

отложенных вычислений при нахождении facto(3) = 3!.

Замечание. С помощью встроенной функции if() предложенный алгоритм удается записать еще короче. Это же касается и многих других примеров.

Для решения конкретной задачи иногда удается построить несколько различных рекурсивных алгоритмов. Например, функцию facto(n) можно было бы определить и так.

По сравнению с прежней реализацией facto() здесь количество рекурсивных вызовов уменьшается практически в 2 раза. В реальных ситуациях подобный фактор может оказаться решающим при выборе того или иного алгоритма.

Используем теперь для вычисления n! cформулированную выше схему 3 (обобщить). Если вместо исходной функции facto(n)=n!, ввести в рассмотрение функцию двух переменных fa(n, l)=l×n! (n=0,1,…), то получим равенства:

fa(n, l)=l×n×(n-1)×…×1=(l×n)×(n-1)!=fa(l×n)×(n-1)!,

fa(1, l)=l , fa(n,1)=n!.

Первое из этих соотношений может служить правилом декомпозиции, второе - определять рекурсивную базу, а третье - показывает, как вычислять n!. Соответствующая рекурсивная программа-функция могла бы выглядеть так:

В чем же отличие этой функции от первого варианта функции facto(n)? Дело в том, в facto(n) формирование n! реализуется при проведении отложенных вычислений, в то же время нахождение fa(n, l) проводится вообще без отложенных вычислений. Особенно наглядно это видно на рисунках 3.1 и 3.2. На шагах 4, 5 и 6, отмеченных на рис. 3.2 жирными цифрами в круглых скобках, происходит лишь передача значений. Иными словами здесь мы имеем повторительную рекурсию.

Рис. 3.2. Схематическое изображение рекурсивных вызовов

при нахождении fa(3,l) = l×3!.

Еще один вариант вычисления n! можно реализовать с помощью рассмотренной ниже в задаче 20 функции Кадью.

3.2 Сложный процент

Задача 2. Вкладчик положил в сбербанк сумму в sum единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию возвращающую величину вклада по истечении n периодов времени (n = 1, 2,).

Решение. Пусть invest(sum,p,n) искомая функция. Для данной задачи вычисления значений invest() можно проводить по формуле

invest(sum,p,n) = sum×(1+p/100)n .

Однако, в учебных целях, нас интересует рекурсивный вариант алгоритма решения задачи. Рекурсию будем осуществлять по параметру n. Тривиальный случай очевиден. Если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 периодов и затем полученную сумму положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:

Контрольные примеры.

Схема рекурсивных вызовов здесь такая же, как при вычислении значений функции facto(n). Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) равно n. При необходимости можно было бы уменьшить это значение до log2(n).

3.3 Степень числа

Задача 3. Пусть a - вещественное число отличное от нуля и n - целое неотрицательное число. Составить программу-функцию возвращающую величину an.

Решение. Приведенная ниже функция power(a,n) дает решение задачи за n рекурсивных вызовов:

Уменьшить количество вызовов можно так. Организуем декомпозицию иначе, представив величину an в виде:

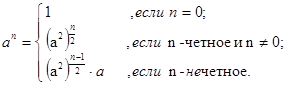
Отсюда сразу же получаем алгоритм вычисления an, требующий не более log2(n) рекурсивных вызовов. Реализуется он функцией pow(a,n):

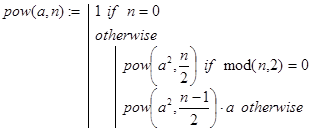
Сумма элементов массива

Задача 4. Составить программу-функцию, возвращающую сумму S компонентов вектора v=(a0,a1,…,an-1)T: S= a0+a1+…+an-1, где n³1 и ap (p=0 n-1) - вещественные или комплексные числа.

Решение. Определение суммы n слагаемых в виде:

S= a0+a1+…+an-1=(a0 +a1+…+an-2)+an-1

рекурсивно по своей сути. Сумма n слагаемых есть сумма первых (n-1)-го слагаемого плюс сумма последнего слагаемого. Этот факт и положен в основу определения функции summa(v), где v=(a0,a1,…,an-1)T.

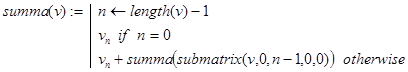
3.4 Произведение элементов массива

Задача 5. Составить программу-функцию, возвращающую произведение P компонентов вектора v=(a0,a1,…,an-1)T: P= a0×a1×…×an-1, где n³1 и ap (p=0 n-1) - вещественные или комплексные числа.

Решение. Определение произведения n сомножителей в виде:

P= a0×a1×…×an-1= (a0×a1×…×an-2)×an-1 ,

как и соответствующее определение суммы, рекурсивно по своей сути. Произведение n сомножителей есть произведение первых (n-1)-го сомножителей умноженное на последний сомножитель. Отсюда и определение функции product(v), где v=(a0,a1,…,an-1)T.

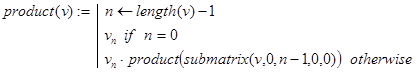
3.5 Числа Фибоначчи

Задача 6. Составить программу-функцию вычисления n-го числа Фибоначчи, исходя из рекуррентного определения этих чисел:

f(0)=f(1)=1, f(n)=f(n-1)+f(n-2) (n=2,3,…).(1)

Решение. Наличие рекуррентного соотношения вида (1) сразу же определяет и базу рекурсии, и способ декомпозиции. Программа-функция fib(n) написана строго в соответствии с определением (1).

Контрольные примеры.

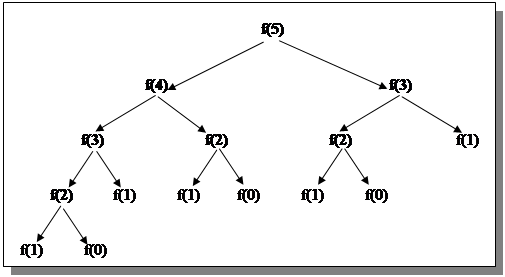
Функция fib(n) вряд ли подходит для вычисления чисел Фибоначчи при больших n. И происходит это потому, что в данном случае с ростом n дерево рекурсивных вызовов очень быстро разрастается. На рис. 3.3 представлена схема рекурсивных вызовов для fib(5) (имя функции обозначено через f).

 Скачать реферат