Рекурсия

Замечание. Моделирование различных операций возможно не только для целых неотрицательных чисел. Их можно было бы определить и для множества всех целых чисел и даже для множества вещественных чисел. Ограничимся рассмотрением одного примера. Напишем рекурсивную программу-функцию нахождения дробной части вещественного числа, если разрешены лишь операции x+1 и x-1. Вот один из возможных дост

аточно ясных вариантов её определения:

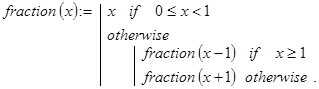
Контрольный пример.

Синтаксические языковые конструкции

Задача 37. Составить программу-функцию проверяющую, является ли данная последовательность символов идентификатором языка Фортран.

Решение. Будем считать, что речь идет о версиях Фортрана, где идентификатор определялся как последовательность из шести заглавных латинских букв и (или) цифр, начинающаяся с буквы и для символов была принята ASCII кодировка. Превратить последовательность символов в вектор соответствующих им ASCII-кодов можно с помощью встроенной функции str2vec(). Например:

Дополнительное ограничение на первый символ идентификатора (буква, но не цифра) усложняет общую проверку (или буква, или цифра). Чтобы действия были стандартными для всех символов, проверку первого из них будем осуществлять на допустимость отдельно в головной программе. Естественно там же располагать и проверку длины слова, которая должна находиться в пределах от 1 до 6. Тогда в подпрограмме останется решить вполне рекурсивную подзадачу: “если первый символ исходного слова не буква и не цифра, то формируем ответ “не идентификатор”. В противном случае, если длина слова равна единице, то возвращаем ответ “идентификатор”, а иначе укорачиваем слово на первый символ и снова решаем эту же подзадачу. Все сказанное и реализуется головной программой identity(word) и рекурсивной подпрограммой iden(v):

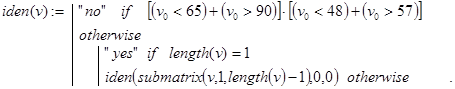
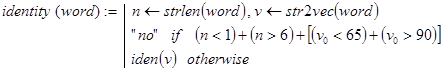
Контрольные примеры.

Замечание. В любом языке программирования все базовые языковые конструкции (идентификаторы, константы, переменные, выражения, метки, типы и т.п.) определяются рекурсивно. Особенно наглядно это видно, когда они представлены с помощью синтаксических диаграмм [7, c. 685-703] или в форме Бэкуса-Наура. Подобные определения в рамках конкретного языка программирования могут служить наборами тренировочных заданий по написанию рекурсивных программ и даже простейших рекурсивных трансляторов.

Приведем пример. Идентификатор в Паскале определяется, как и в Фортране, но без ограничений на длину последовательности символов. С помощью синтаксической диаграммы это выглядит так, как это указано на рис.3.7., а в форме Бэкуса-Наура следующим образом (значок “::=” читается как “есть по определению”):

<идентификатор>::=<буква>

<идентификатор>::=<идентификатор><буква>

<идентификатор>::=<идентификатор><цифра>

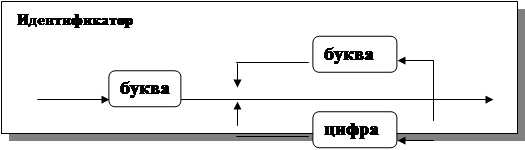Рис. 3.7. Синтаксическая диаграмма идентификатора (Паскаль)

И в том и в другом случаях идентификатор определяется сам через себя.

3.28 Проблемная ситуация

Задача 38. При любом ли натуральном n ли рекурсивная функция

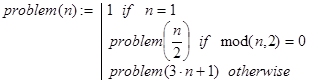
равна 1?

Решение. Хотя данная строка и начата со слова “решение”, ответа на поставленный вопрос мы не знаем и, по-видимому, на сегодняшний день его не знает никто. Более того, неизвестно, для любого ли n problem(n) вычисляется за конечное число шагов. Рассмотренную задачу называют 3×n+1 проблемой. Мы включили её в список задач для того, чтобы обратить внимание читателя на следующий факт. Достаточно простые с виду рекурсивные определения функций могут таить в себе глубокие проблемы, решения которых лежат совсем не на поверхности. Тем не менее, конкретные вычисления problem(n) при разных n приводят к одному и тому же значению, равному 1. Ниже приведена рекурсивная программа для проверки истинности утверждения “problem(n)=1” при значениях n из диапазона k1 k2.

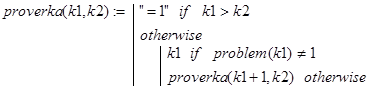
Контрольные примеры.

6. Задача Иосифа Флавия

С именем известного историка первого века Иосифа Флавия связывают следующую задачу-легенду. В ходе иудейской войны он в составе отряда из 41 воина был загнан римлянами в пещеру. Не желая сдаваться, осажденные воины решили покончить жизнь самоубийством и разработали для этого следующую процедуру. Они выстроились в круг и, начиная отсчет с конкретной позиции, каждый третий должен был убивать себя, пока не останется ни одного человека. Математически одаренный Иосиф считал подобный конец бессмысленным и потому поставил себя и своего друга на такие позиции, что после серии из 39 самоубийств они остались вдвоем, чем и спасли себе жизнь. Что это были за позиции?

Дадим этой задаче-легенде более точную и обобщенную формулировку, освободившись от суицида. При этом будем искать рекурсивные решения двух ниже приведенных задач, различающихся завершением соответствующей процедуры. Подробнее рекурсия как метод решения практических задач обсуждается в следующем параграфе.

Задача 1. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, . каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока чисел не станет меньше k. Определить оставшиеся числа.

Задача 2. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, . каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока не останется одно число. Определить его.

A. Решение первой задачи Флавия при k=2.

Ниже рассмотрены три варианта A1-A3 решения задачи 1 при k=2, опирающиеся на разные идеи.

A1. Если n=2×s, то после первого прохода по кругу останутся числа: 1, 3, . 2×s-1 и следующий проход начнется с вычеркивания числа 3. Это все равно, как если бы мы начинали с s последовательных натуральных чисел от 1 до s, но каждое уцелевшее число удваивали и результат уменьшали на 1. Отсюда, если fla1(n) - функция, решающая поставленную задачу, то fla1(1)=1 и

 Скачать реферат