Рекурсия

Рис. 3.3. Схематическое изображение рекурсивных вызовов при

нахождении f(5)

Для ускорения вычислений можно было бы учесть, что

Это приводит к следующей рекурсивной программе функции:

Отметим, что теперь количество рекурсивных вызовов для fiboo(n) имеет порядок равный log2(n) и, скажем, fiboo(200) в символьной форме вычисляется практически мгновенно.

Контрольные примеры.

fiboo(0)=1 fiboo(1)=1 fiboo(10)=89

fiboo(200) ® 453973694165307953197296969697410619233826

3.6 Алгоритм Ламберта вычисления e

Задача 7. Составить программу вычисления приближения к основанию натуральных логарифмов, то есть к числу е, используя следующий алгоритм Ламберта:

Решение. Указанный алгоритм предложен Ламбертом в 1766 году [6, с.70]. Организовать по нему рекурсивные вычисления труда не составляет. Здесь величины a(k) и b(k) задаются рекуррентными соотношениями, похожими на определение чисел Фибоначчи, но нелинейными. Однако это обстоятельство не привносит каких-либо дополнительных затруднений в программную реализацию соответствующих функций. Дело в том, что задание последовательности любыми рекуррентными соотношениями сразу решает проблему триады: осуществлена параметризация задачи, выделена база и задана декомпозиция.

Программа e(k) приближенно вычисляет e, обращаясь к рекурсивным функциям-подпрограммам a(k) и b(k):

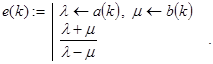
Учитывая, что последовательности a(k) и b(k) (k=0,1,2, …) определяются весьма схожим образом, можно построить одну общую функцию двух переменных для вычисления их членов. Отсюда ещё один вариант решения поставленной задачи:

Контрольный пример.

Мы видим, что уже е(5) » e с точностью до 9 знаков после десятичной точки, а начиная с e(8) уже все 15 знаков после точки верные. Если была бы необходимость вычислять по алгоритму Ламберта число e с большей точностью, то пришлось бы программно реализовывать арифметику длинных чисел.

Замечание. Предложенные варианты вычисления e можно было бы сделать существенно более эффективными, организовав в них динамические базы, пополняемые в процессе вычислений уже найденными значениями. Тем самым, исключив повторные вычисления элементов последовательностей, можно было бы вычислять a(k), b(k) и d(k,t) за k рекурсивных обращений.

3.7 Наибольший общий делитель

Задача 8. Составить программу-функцию возвращающую наибольший общий делитель двух натуральных чисел x и y.

Решение. Обозначим через nod(x,y) – наибольший общий делитель x и y. Известно, что

(2)

На этих утверждениях базируется известный итеративный алгоритм Евклида, нахождения наибольшего общего делителя двух целых чисел. Внимательный взгляд на соотношения (2) приводит нас к убеждению, что фактически мы имеем рекурсивное определение функции nod(x,y). На языке Mathcad это надо было бы записать так.

Контрольные примеры.

Обобщим решенную задачу, составив программу-функцию, возвращающую наибольший общий делитель нескольких натуральных чисел ap (p=0 n-1, n³1), являющихся компонентами вектора v=(a0,a1,…,an-1)T.

Обозначим через nodd(a0,a1,…,an-1) – наибольший общий делитель чисел ap (p=0 n-1). Поскольку

nodd(a0,a1,…,an-1)=nod(nodd(a0,a1,…,an-2),an-1) ,

то соответствующая программа-функция, вычисляющая nodd(v) будет выглядеть так:

Контрольный пример.

3.8 Наименьшее общее кратное

Задача 9. Составить программу-функцию, возвращающую наименьшее общее кратное натуральных чисел ap (p=0 n-1, n³2), являющихся компонентами вектора v=(a0,a1,…,an-1)T.

Решение. Обозначим через nok(a0,a1,…,an-1) – наименьшее общее кратное чисел ap (p=0 n-1). Известно, что

и

Поэтому соответствующую программу-функцию можно было бы записать так:

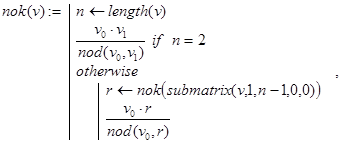
где nod(x,y) - функция нахождения наибольшего общего делителя натуральных x и y.

Контрольный пример.

Функцию nok() можно записать в следующей более компактной форме:

3.9 Биномиальные коэффициенты

Задача 10. Составить программу-функцию вычисления биномиальных коэффициентов С(n,m), где n m - целые и 0£m£n.

Решение. Известно, что

Отсюда и вытекает справедливость следующего рекурсивного определения С(n,m):

Обратите внимание на то, что здесь мы имеем рекурсию сразу по двум аргументам.

Опираясь на функцию C(n,m) как на подпрограмму, построим функцию binom(n,k), возвращающую для целого n³0 вектор из k последовательных биномиальных коэффициентов: С(n,0), C(n,1),…,C(n,k) (k£n).

Решение данной задачи можно записать так:

Контрольные примеры.

Замечание. Для отыскания всех биномиальных коэффициентов при заданном n не обязательно вычислять binom(n,n). Учитывая, что C(n,k)=C(n,n-k), достаточно вычислить binom(n,(n-mod(n/2))/2).

И еще один способ вычисления биномиальных коэффициентов. Рекурсивная программа-функция tripas(n) вычисляет треугольник Паскаля, то есть значения величин C(i,j) для (0£i£n , 0£j£i), исходя из формул непосредственно определяющих и декомпозицию и базу:

 Скачать реферат