Разработка лекционной демонстрации "Изучение механизма формирования ударной волны" для курса "Молекулярная физика"

Задачи лекции, реализующие основной замысел:

а) состав и последовательность задач;

б) характер задач;

в) средства, необходимые студентам для решения указанных задач;

г) эмоциональные позиции и отношения, которые формируются преподавателем у слушателей при решении поставленных задач.

а) Состав и последовательность задач:

1) Сформировать представление о процессах, изучаемы

х в данной дисциплине;

2) Познакомиться с основными понятиями;

3) Рассмотреть основные методы изучения и решения вопросов и задач, изучаемых в данной дисциплине;

б) Характер задач:

Информационный (дать информационный материал по данной теме и закрепить основные понятия);

Мотивационный (сформировать познавательный интерес к содержанию учебного материала);

Ориентировочный (дать основы для дальнейшего усвоения учебного материала);

Воспитательный (помочь выработать у студентов стремление к самостоятельной работе и всестороннему овладению специальностью, развивать интерес к учебной дисциплине, содействовать активизации мышления студентов);

в) Средства, необходимые студентам для решения указанных задач:

Основные понятия и формулы по данной теме; раздаточный материал; список рекомендованной литературы;

г) Эмоциональные позиции и отношения, которые формируются преподавателем у слушателей при решении поставленных задач:

Нужно суметь сосредоточить внимание студентов на восприятие и понимание указанного материала, а также настроить их на внутреннюю мыслительную и эмоциональную активность в ответ на действия преподавателя и поступающую от него информацию. Необходимо постоянно наблюдать за аудиторией и чувствовать ее.

Теоретические сведения по теме “Ударные волны”

Введение в газодинамику понятия об ударной волне

Рассмотрим покоящийся газ с постоянными плотностью и давлением , , слева ограниченный плоским поршнем, и предположим, что в начальный момент поршень начал сжимать газ с постоянной скоростью, которую будем теперь обозначать через .

Как было показано в предыдущем параграфе, попытка найти непрерывное решение для этой задачи приводит к физически бессмысленному результату. Поскольку задача автомодельная (не содержит никаких характерных масштабов длины и времени), единственные решения, удовлетворяющие уравнениям газовой динамики,— это тривиальное решение, в котором все величины, , p постоянны, и решение типа центрированной простой волны. Таким образом, остается одна единственная возможность построить решение, удовлетворяющее граничным условиям задачи — в невозмущенном газе = 0, = , p = ; в области газа, прилегающей к поршню, скорость газа равна скорости поршня,— это выбросить физически бессмысленную область II и непосредственно сомкнуть области постоянного течения I и III, предположив, что в точке смыкания газодинамические величины терпят разрыв, как показано на рис. 2.1.

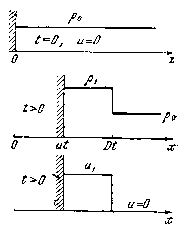
Рисунок 2.1 - Профили плотности и скорости в ударной волне

Вообще говоря, законы сохранения массы, импульса и энергии, которые положены в основу уравнений динамики невязкого и нетеплопроводного газа, не предусматривают обязательную непрерывность газодинамических величин. Эти законы были сформулированы ранее в форме дифференциальных уравнений просто потому, что с самого начала предполагалась непрерывность течения. Но эти же законы можно применить и к областям, в которых газодинамические величины испытывают разрыв. С математической точки зрения разрыв можно рассматривать как предельный случай очень больших градиентов газодинамических величин, когда толщина слоя, в котором происходит конечное изменение этих величин, стремится к нулю. Поскольку в динамике невязкого и нетеплопроводного газа, т.е. при условии, что мы отвлекаемся от молекулярной структуры вещества, нет никаких характерных длин, постольку не ограничены возможности существования сколь угодно тонких переходных слоев, в пределе сводящихся к разрыву. Эти разрывы и представляют собой ударные волны.

Найдем неизвестные величины: плотность и давление газа в сжатой области , , а также скорость распространения разрыва по невозмущенному веществу D, исходя из общих законов сохранения массы, импульса и энергии, выполнение которых не подлежит сомнению. Параметры невозмущенного газа , и скорость поршня u, с которой совпадает скорость газа, будем считать известными. К моменту t в столбе с сечением в 1 см2 движение охватывает массу газа, равную Dt. Эта масса занимает объем (D — u) t, т.е. плотность сжатого газа , удовлетворяет условию:

(2.1)

Масса приобретает количество движения - u, которое по закону Ньютона равно импульсу сил давления. Результирующая сила, действующая на сжатый газ, равна разности давлений со стороны поршня и со стороны невозмущенного вещества, т.е.

(2.2)

Наконец, приращение суммы внутренней и кинетической энергий сжатого газа равно работе внешней силы, толкающей поршень :

(2.3)

Сокращая в этих равенствах время t, получим систему трех алгебраических уравнений для определения трех неизвестных величин , , D через известные u, , (термодинамическая связь , конечно, предполагается известной).

Преобразуем эти уравнения таким образом, чтобы с правой стороны равенств стояли только величины, относящиеся к области перед разрывом, а с левой — параметры газа за разрывом. Для этого заметим, что если D — скорость распространения разрыва по неподвижному газу, то = - D — скорость, с которой невозмущенный газ втекает в разрыв, a D - u — скорость распространения разрыва относительно движущегося за ним газа, т.е. — это скорость, с которой газ вытекает из разрыва. Вводя эти обозначения в уравнения, запишем закон сохранения массы: