Расчет показателей эконометрики
Система нормальных уравнений составит
![]()
Используем следующие формулы для нахождения параметров:
![]() = 2,799
= 2,799
![]() 305,6 - 2,799*5,47 = 15,251
305,6 - 2,799*5,47 = 15,251
Уравнение парной линейной регрессии:
h=15 height=32 src="images/referats/9778/image010.png">= 15,251 + 2,799* x
Величина коэффициента регрессии b = 2,799 означает, что с ростом инвестиций в основной капитал на 1 тыс. руб. доля ВРП на душу населения растет в среднем на 2,80 %-ных пункта.
Знак при свободном члене уравнения положительный, следовательно связь прямая.
3. Рассчитаем линейный коэффициент корреляции:
 или
или ![]()
где ![]() ,
, ![]() - средние квадратические отклонения признаков x и y, соответственно
- средние квадратические отклонения признаков x и y, соответственно
Так как ![]() = 2,23,
= 2,23, ![]() = 7,098, то
= 7,098, то
![]() = 0,879, что означает тесную прямую связь рассматриваемых признаков
= 0,879, что означает тесную прямую связь рассматриваемых признаков
Коэффициент детерминации составит
![]() = 0,773
= 0,773
Вариация результата (y) на 77,3% объясняется вариацией фактора (x). На долю прочих факторов, не учитываемых в регрессии, приходится 22,7%.
4. Средняя ошибка аппроксимации (![]() ) находится как средняя арифметическая простая из индивидуальных ошибок
) находится как средняя арифметическая простая из индивидуальных ошибок
 =
= ![]() =7,9%,
=7,9%,
(см. последнюю графу расчетной табл. 1.1.).
Ошибка аппроксимации показывает хорошее соответствие расчетных (![]() ) и фактических (y) данных: среднее отклонение составляет 7,9%.
) и фактических (y) данных: среднее отклонение составляет 7,9%.
5. Стандартная ошибка регрессии рассчитывается по следующей формуле:
 ,
,
где m – число параметров при переменных x.
В нашем примере стандартная ошибка регрессии
![]() = 3,782
= 3,782
6. Оценку статистической значимости построенное модели регрессии в целом производится с помощью F-критерия Фишера. Фактическое значение F-критерия для парного линейного уравнения регрессии определяется как
F = ![]()
где Сфакт = ![]() - факторная, или объясненная регрессия, сумма квадратов; Сост =
- факторная, или объясненная регрессия, сумма квадратов; Сост = ![]() - остаточная сумма квадратов;
- остаточная сумма квадратов;
![]() - коэффициент детерминации.
- коэффициент детерминации.
В нашем примере F-критерий Фишера будет равен (см. приложение №1):
F = ![]() = 27,233
= 27,233
Табличное значение F-критерия при числе степеней свободы 1 и 8 и уровне значимости 0,05 составит: 0,05 F1,8 = 5,32, т. е. фактическое значение F (Fфакт = 27,233) превышает табличное (Fтабл = 5,32), и можно сделать вывод, что уравнение регрессии статистически значимо. Следовательно гипотеза Н0 отклоняется.
Чтобы оценить значимость отдельных параметров уравнения, надо по каждому из параметров определить его стандартные ошибки: mb и ma.
Стандартная ошибка коэффициента регрессии определяется по формуле:
mb =  =
=
где S2 – остаточная дисперсия на одну степень свободы.
Стандартная ошибка параметра a определяется по формуле:
ma = 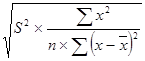 .
.
Для нахождения стандартных ошибок строим расчетную таблицу (см. приложение №1).
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
mb =![]() = 0,536.
= 0,536.
Величина стандартной ошибки параметра a составила:
ma = ![]() = 3,168
= 3,168
Для оценки существенности коэффициента регрессии и параметра a их величины сравниваются с их стандартными ошибками, т. е. определяются фактические значения t-критерия Стьюдента:
tb =![]() , ta =
, ta = ![]() .
.
Для нашего примера
tb =![]() = 5,222, ta =
= 5,222, ta = ![]() = 4,814
= 4,814
Фактические значения t-критерии превосходят табличные значения:
tb =5,222 > tтабл = 2,306; ta = 4,814 > tтабл = 2,306
Поэтому гипотеза Н0 отклоняется, т. е. a и b не случайно отличаются от нуля, а статистически значимы.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Для расчета точечного прогноза ![]() подставим в уравнение регрессии заданное значение факторного признака
подставим в уравнение регрессии заданное значение факторного признака ![]() . Если прогнозное значение инвестиций в основной капитал составит:
. Если прогнозное значение инвестиций в основной капитал составит:
![]() = 9,4*0,8 = 7,52 тыс. руб
= 9,4*0,8 = 7,52 тыс. руб
Тогда прогнозное значение ВРП на душу населения составит:
![]() = 15,251 + 2,799* 7,52 = 36,299 тыс. руб.
= 15,251 + 2,799* 7,52 = 36,299 тыс. руб.
Доверительный интервал прогноза определяется с вероятностью (0,95) как
![]()
![]() ,
,
где tтабл – табличное значение t-критерия Стьюдента для уровня значимости ![]() (1-0,95) и числа степеней свободы (n-2) для парной линейной регрессии;
(1-0,95) и числа степеней свободы (n-2) для парной линейной регрессии; ![]() - стандартная ошибка точечного прогноза, которая рассчитывается по формуле:
- стандартная ошибка точечного прогноза, которая рассчитывается по формуле:
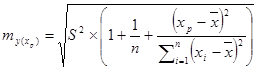
В нашем примере стандартная ошибка прогноза составила
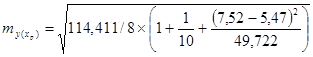 = 4,116
= 4,116
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
![]() =
=![]() = 2,306 * 4,116 = 9,491.
= 2,306 * 4,116 = 9,491.
Доверительный интервал прогноза
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
