Расчет показателей эконометрики

Критерий Дарбина – Уотсона равен = 1,604.

Коэффициент автокорреляции равен = - 0,096.

Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При n = 12 месяцев и

m = 1 (число факторов) нижнее значение d’ равно 0,97, а верхнее – 1,33. Фактическое значение d=1,604 > d’=1,33, следовательно, автокорреляция остатков отсутствует.

Чтобы проверить значимость отрицательного коэффициента автокорреляции, сравним фактическое значение d с (4-dL ) и (4-dU):

Из таблицы видно, что в обоих случаях фактическое значение меньше сравниваемых. Это означает отсутствие в остатках автокорреляции.

Так же принято считать, что если фактическое значение d близко к 2, то автокорреляции остатков нет. В нашем примере это совпадает.

4. В соответствии с интерпретацией параметров линейного тренда, каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста. Тогда:

а) Точечный прогноз составит:

Точечный прогноз по уравнению тренда – это расчетное значение переменной , полученное путем подстановки в уравнение тренда значений

(n – длина динамического ряда, l – период упреждения).

= 2,927 + 0,153* (12 + 1) = 4,916 (тыс. руб.)

ожидаемый уровень номинальной заработной платы на январь следующего года.

б) Интервальный прогноз составит:

Доверительный интервал прогноза определяется с вероятностью 0,95, как:

;

где, tтабл=2,2281 - табличное значение t-критерия Стьюдента для уровня значимости α=0,05 и числа степеней свободы (n – 2 = 12 – 2 = 10); - стандартная ошибка точечного прогноза, которая рассчитывается по формуле:

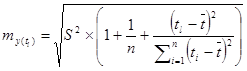
Данные необходимые для расчета представим в таблице.

Таблица 4.4 Расчетная таблица

 Скачать реферат