Расчет показателей эконометрики

Sобщ = = 1350,5 * 26 = 35113;

Sфакт = = 1350,5 * 26 * 0,956 = 33568,028;

Sфакт x1 == 1350,5 * 26 * 0,7172 = 18051,207;

Sфакт x2 = Sфакт - Sфакт x1 = 33568,028 – 18051,207 = 15516,821;

Sо

ст = = Sобщ - Sфакт = 35113 – 33568,028 = 1544,972;

Fфакт = = = 249,864;

Fфактx1 = = = 268,728;

Fчастнx2 = = = 230,999.

= 16784,014;

= 15516,821;

= 18051,207

Включение в модель фактора x2 после фактора x1 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т. е. следствием дополнительного включения в модель систематически действующего фактора x2, так как Fчастнx2 = 230,999 > Fтабл = 4,28.

8. Оценка с помощью t-критерия Стьюдента значимости коэффициента b2 связана с сопоставлением его значения с величиной его случайной ошибки: mb2.

Расчет значения t-критерия Стьюдента для коэффициента регрессии линейного уравнения находится по следующей формуле:

= 15,199.

При α = 0,05; df = n-m-1 = 26-2-1 = 23; tтабл = 2,07. Сравнивая tтабл и tфакт, приходим к выводу, что так как = 15,199 > 2,07 = tтабл, коэффициент регрессии b2 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе.

9. Стандартная ошибка регрессии рассчитывается по следующей формуле:

= = 8,196.

Задача 3

Рассматривается модель вида

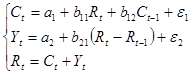
где

Сt – расходы на потребление в текущий период,

Сt-1 – расходы на потребление в предыдущий период,

Rt – доход текущего периода,

Rt-1 – доход предыдущего периода,

Yt – инвестиции текущего периода.

Ей соответствует следующая приведенная форма (построена по районам области)

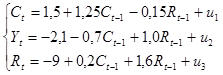
Задание

1. Проведите идентификацию модели.

2. Укажите способы оценки параметров каждого уравнения структурной модели.

3. Найдите структурные коэффициенты каждого уравнения, если известны следующие данные:

Решение

1. Модель имеет три эндогенные Н (Сt, Yt, Rt). Причем переменная Rt задана тождеством. Поэтому практически статистическое решение необходимо только для первых двух уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределенные D (Сt-1, Rt-1) переменные.

Проверим каждое уравнение системы на необходимое и достаточное условия идентификации.

Проверим необходимое условие идентификации для уравнений модели.

I уравнение.

Н: эндогенных переменных – 2 (Сt, Rt), отсутствующих предопределенных переменных – 1 (Rt-1).

Следовательно, по счетному правилу D + 1 = H (1 + 1 = 2) уравнение идентифицируемо.

II уравнение.

Н: эндогенных переменных – 1 (Yt); переменная Rt в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной Rt-1.

отсутствующих предопределенных переменных – 1 (Сt-1).

Следовательно, по счетному правилу D + 1 > H (1 + 1 > 1) уравнение сверхидентифицировано.

III уравнение.

Третье уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.

Следовательно, рассматриваемая в целом структурная модель сверхидентифицируема по счетному правилу.

 Скачать реферат