Математическая модель в пространстве состояний линейного стационарного объекта управления

Числовое значение найденных моментов:

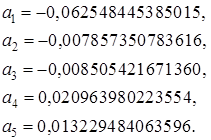
Моментные функции:

Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).

Из этого следует, что функционал, значения , управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).

Оптимальное управление имеет вид:

Проверим правильность полученного решения.

Эталонные значения координат в начальный и конечный момент времени:

,

,

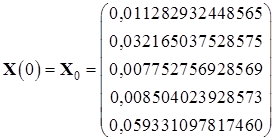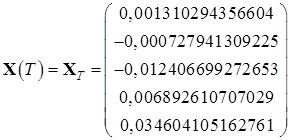
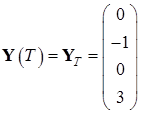
Найденные значения координат в начальный и конечный момент времени:

,

,

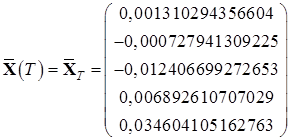
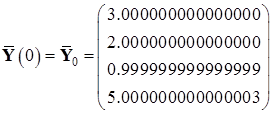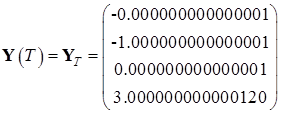
Вычислим погрешность полученных результатов:

,

,

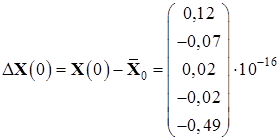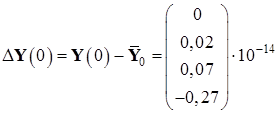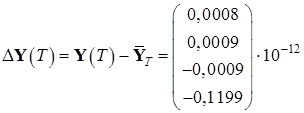
Ниже представлены графики полученного решения с помощью скрипта Optimal_L_problem_moments.m.

Рис. 18. Графики фазовых координат системы при переходе из в .

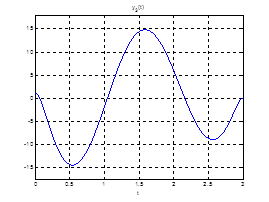
Рис. 19. Графики выходных координат системы при переходе из в .

Рис.20. График оптимального управления .

Выводы: Задача перевода системы из начальной точки в конечную с помощью L-проблемы моментов в пространстве состояний и в пространстве вход-выход была решена с точностью до 12-го знака после запятой. Результаты, полученные при переводе системы из начальной точки в конечную, полностью совпадают.

4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)

Система имеет вид:

с начальными условиями:

,

.

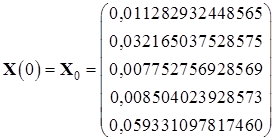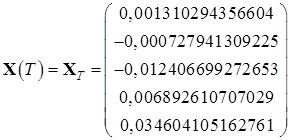
Составим матрицу управляемости и проверим управляемость системы:

.

Составим грамиан управляемости для данной системы:

Найдем грамиан по формуле:

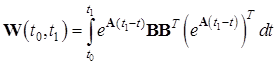
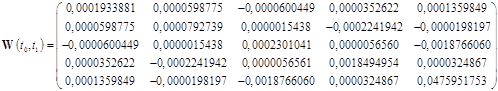
Тогда управление имеет вид:

.

или

Ниже представлен график оптимального управления полученного с помощью скрипта Gramian_Uprav.m.:

Рис.21. График оптимального управления .

Графики фазовых координат аналогичны, как и в оптимальной L – проблеме моментов.

Сравним управление, полученное в начальной и конечной точках в пунктах 3 и 4 соответственно:

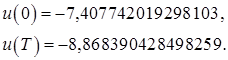и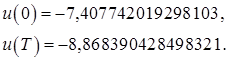

Выводы: Как видно, значения граничных управлений совпадают. А это значит, что задача перевода объекта из начального состояния в конечное решена с высокой степенью точности и с минимальной энергией.

Графическое сравнение оптимальных управлений из пунктов 3 и 4:

Рис.21. Сравнение графиков оптимального управления .

5. Аналитическое конструирование оптимальных регуляторов (АКОР)

5.1 Стабилизации объекта управления на полубесконечном интервале времени

Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме

Необходимо получить закон управления

минимизирующий функционал вида

Начальные условия для заданной системы

Моменты времени фиксированы. Матрицы — симметричные неотрицательно определенные:

матрица — положительно определенная:

Матричное дифференциальное уравнение Риккати имеет вид:

 Скачать реферат