Математическая модель в пространстве состояний линейного стационарного объекта управления

Найдем матрицу управляемости:

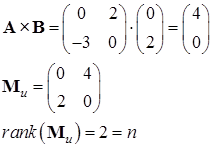
Ранг матрицы управляемости равен порядку системы, следовательно, данная система является управляемой.

следовательно .

Собственные числа матрицы найдем из уравнения :

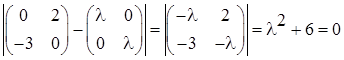
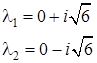
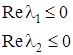
Действительные части собственных значений матрицы являются неположительными, следовательно, все условия управляемости выполнены.

2. Ссылаясь на решение задачи быстродействия из ДЗ№2 по СУЛА «Решение задачи быстродействия» имеем:

Запишем зависимости , , полученные при решении систем дифференциальных уравнений:

:

:

:

:

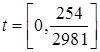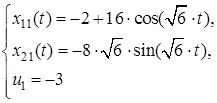
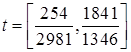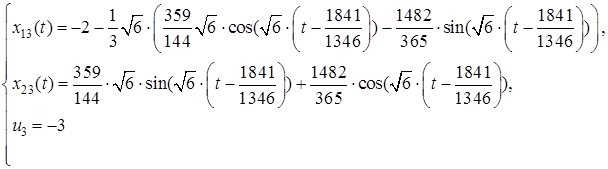
Перейдем к дискретной модели заданной системы. Имеем

(4)

где шаг дискретизации и соответствующие матрицы

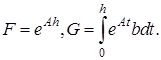(5)

Пусть управление ограничено интервальным ограничением

(6)

Тогда на шаге имеем

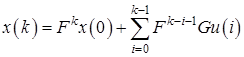(7)

Известны начальная и конечная точки

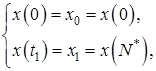
где – оптимальное число шагов в задаче быстродействия.

Решается задача быстродействия

а) Формирование задачи быстродействия как задачи линейного программирования

Конечная точка в дискретной модели представлена в виде

(8)

Получаем – равенств

(9)

Для приведения ограничений (9) к канонической форме сделаем необходимое преобразование в правой и левой частях, чтобы правые части были неотрицательными (если правая часть меньше нуля, то домножаем на (-1) левую и правую части). Отметим проведенные изменения точкой в правом верхнем углу соответствующих векторов

. (10)

Для того чтобы получить необходимый допустимый базис для задачи линейного программирования, добавим формально остаточные искусственные переменные (). Таким образом, уравнения (10) представляются в виде

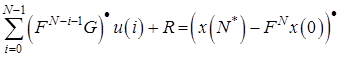(11)

Так как текущее управление – управление имеет любой знак, то сделаем необходимую замену

Тогда уравнения (11) примут вид

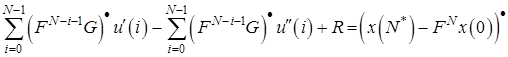(12)

Введем остаточные переменные в ограничения на управление

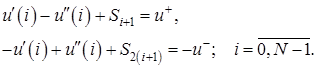(13)

При объединении выражений (12) и (13) получаем ограничений.

Начальный допустимый базис состоит из остаточных и остаточных искусственных переменных

Формируем целевую функцию (по второму методу выбора начального допустимого базиса)

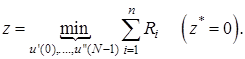(14)

б) Решение задачи быстродействия

Предположим, что , где – оптимальное число шагов. Так как значение нам неизвестно (но известно точно), выбираем некоторое начальное и решаем задачу линейного программирования (12)-(14).

При этом

Общее число столбцов в симплекс-таблице:

Число базисных переменных:

Сформируем строку. Имеем

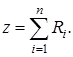
Выразим из уравнения (12) начальные базисные переменные

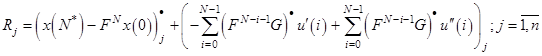
и подставим в целевую функцию. Получим – строку

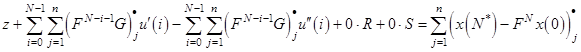(15)

Решаем задачу (12) – (14) симплекс-методом.

В случае,

если , – малое число

иначе

1) если увеличить и целое,рвернуться к первому шагу формирования задачи линейного программирования;

 Скачать реферат